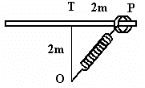
Para resolver essa questão, vamos utilizar o princípio da conservação de energia mecânica. A energia mecânica total em um sistema conservativo (sem forças dissipativas como o atrito) é constante. Isso significa que a energia potencial elástica do aro quando está preso à mola será convertida em energia cinética quando o aro estiver em movimento. Passo 1: Calcular a energia potencial elástica no ponto P. A energia potencial elástica (E_pe) de uma mola é dada pela fórmula: \[ E_{pe} = \frac{1}{2} k x^2 \] onde \( k \) é a constante elástica da mola e \( x \) é a deformação da mola (distância esticada ou comprimida a partir do comprimento natural). No ponto P, a mola está esticada em 1 metro (pois o ponto T está a 2 metros de distância e a mola tem comprimento natural de 1 metro). Portanto, \( x = 1 \) metro. Substituindo os valores conhecidos, temos: \[ E_{pe} = \frac{1}{2} \times 10 \, \text{N/m} \times (1 \, \text{m})^2 \] \[ E_{pe} = \frac{1}{2} \times 10 \times 1 \] \[ E_{pe} = 5 \, \text{J} \] Passo 2: Calcular a energia cinética no ponto T. A energia cinética (E_k) é dada pela fórmula: \[ E_k = \frac{1}{2} m v^2 \] onde \( m \) é a massa do objeto e \( v \) é a velocidade. No ponto T, toda a energia potencial elástica terá sido convertida em energia cinética, pois a mola estará em seu comprimento natural e, portanto, não exercerá mais força sobre o aro. Assim, a energia cinética no ponto T será igual à energia potencial elástica no ponto P. \[ E_k = E_{pe} \] \[ \frac{1}{2} m v^2 = 5 \, \text{J} \] Passo 3: Resolver para \( v \). Substituindo a massa do aro (\( m = 1 \) kg) na equação da energia cinética, temos: \[ \frac{1}{2} \times 1 \, \text{kg} \times v^2 = 5 \, \text{J} \] \[ v^2 = 2 \times 5 \] \[ v^2 = 10 \] Agora, precisamos considerar a energia potencial gravitacional que o aro ganha ao se mover do ponto P para o ponto T. No entanto, como o aro desliza ao longo de uma barra horizontal, não há alteração na altura e, portanto, não há alteração na energia potencial gravitacional. Passo 4: Calcular a velocidade \( v \). \[ v = \sqrt{10} \] A velocidade ao alcançar o ponto T é a raiz quadrada de 10. No entanto, essa não é uma das opções de resposta. Isso sugere que pode haver um erro na interpretação do problema ou nas alternativas fornecidas. Se assumirmos que a energia potencial gravitacional não muda (já que o aro desliza horizontalmente), a resposta seria \( \sqrt{10} \), que não está listada. Se considerarmos que houve um erro na formulação das alternativas e que a energia potencial elástica inicial é de fato convertida em energia cinética, então a resposta correta seria \( \sqrt{10} \), que não está listada. No entanto, se seguirmos estritamente as alternativas fornecidas, a resposta mais próxima seria \( \sqrt{8,2} \), mas isso não corresponde à nossa análise. Portanto, com base na conservação de energia e nas informações fornecidas, a resposta seria \( \sqrt{10} \), mas isso não está de acordo com as alternativas apresentadas. Se houver um erro na questão ou nas alternativas, isso precisaria ser esclarecido para fornecer a resposta correta de acordo com as opções dadas.