Questão sobre Ondas: Experiência de Young
Fonte: IME-2FASE
Disciplina Física
Física
Assunto Ondas: Experiência de Young
Ondas: Experiência de Young
Dificuldade Médio
Médio
(IME-2FASE 2016) - Questão Médio de Física
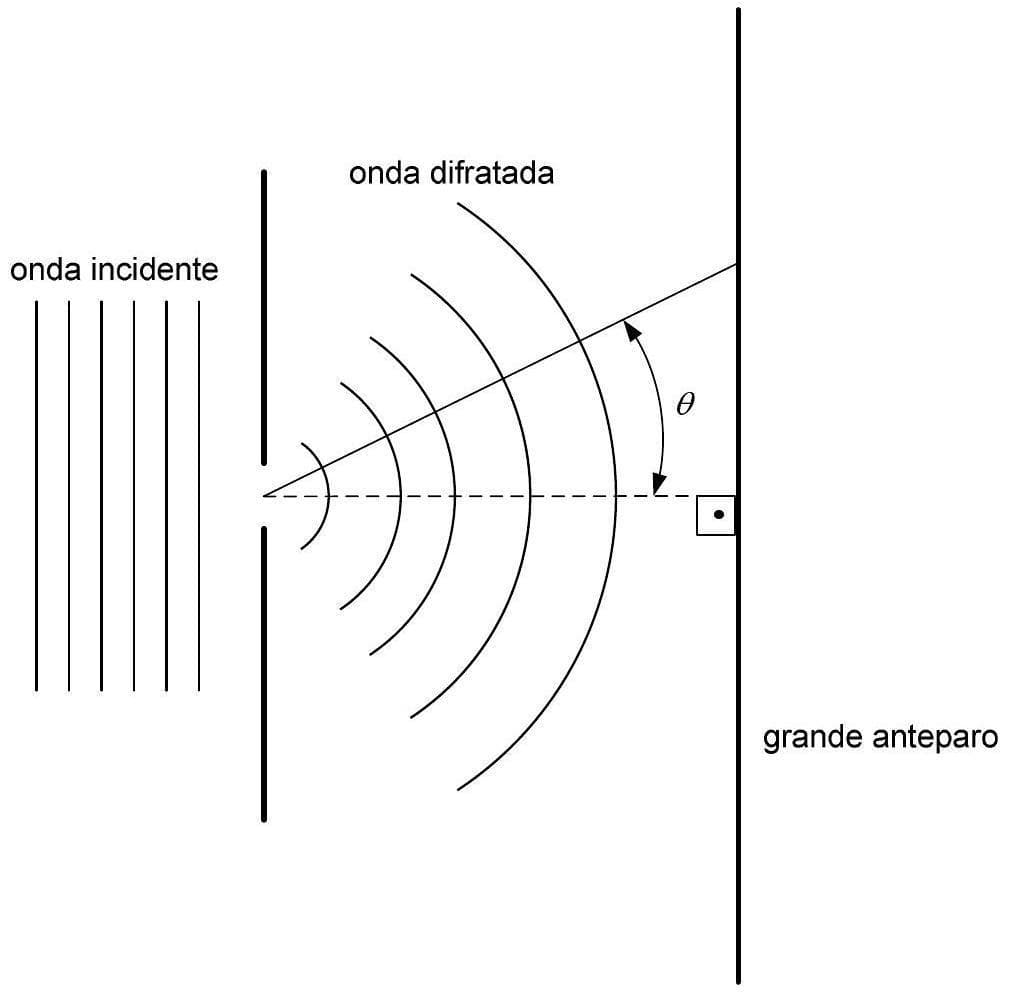
Gabarito
A difração de uma fenda simples produz mínimos de intensidade em ângulos $\theta$ que satisfazem a condição: $a \sin(\theta) = m \lambda$ onde: * $a$ é a largura da fenda. * $\theta$ é o ângulo do $m$-ésimo mínimo em relação ao centro do padrão de difração. * $m$ é a ordem do mínimo ($m = \pm 1, \pm 2, \pm 3, \ldots$). * $\lambda$ é o comprimento de onda da luz. Dados do problema: * Comprimento de onda da luz, $\lambda = 510 \text{ nm}$. * Para um dos mínimos, $\sin(\theta) = \frac{3}{4}$. Substituindo os valores conhecidos na equação dos mínimos: $a \left(\frac{3}{4}\right) = m (510 \text{ nm})$ $a = \frac{4m \times 510 \text{ nm}}{3}$ $a = 4m \times 170 \text{ nm}$ $a = 680m \text{ nm}$ (Equação 1) O problema afirma que "são observados apenas cinco mínimos de intensidade de cada lado do máximo central". Isso significa que os mínimos de ordem $m=1, 2, 3, 4, 5$ são observáveis, mas o mínimo de ordem $m=6$ não é. Para que o $m=6$ mínimo não seja observável, seu ângulo $\theta_6$ teria que ser maior que $90^\circ$, o que significa que $\sin(\theta_6)$ seria maior que 1 (ou não definido no contexto real de observação). Portanto, para $m=6$: $a \sin(\theta_6) = 6 \lambda$ Para que não seja observável, $\sin(\theta_6) > 1$: $\frac{6 \lambda}{a} > 1 \implies a < 6 \lambda$ Substituindo $\lambda = 510 \text{ nm}$: $a < 6 \times 510 \text{ nm}$ $a < 3060 \text{ nm}$ (Condição 1) Agora, para que o $m=5$ mínimo seja observável, seu ângulo $\theta_5$ deve ser menor ou igual a $90^\circ$, o que significa que $\sin(\theta_5) \le 1$. Para $m=5$: $a \sin(\theta_5) = 5 \lambda$ $\sin(\theta_5) = \frac{5 \lambda}{a}$ Para que seja observável, $\sin(\theta_5) \le 1$: $\frac{5 \lambda}{a} \le 1 \implies a \ge 5 \lambda$ Substituindo $\lambda = 510 \text{ nm}$: $a \ge 5 \times 510 \text{ nm}$ $a \ge 2550 \text{ nm}$ (Condição 2) Juntando as Condições 1 e 2, temos: $2550 \text{ nm} \le a < 3060 \text{ nm}$ Agora, vamos usar a Equação 1 ($a = 680m \text{ nm}$) e as condições para determinar o valor de $m$. O $m$ na Equação 1 deve ser um dos valores $1, 2, 3, 4, 5$, já que $\sin(\theta) = 3/4$ corresponde a "um dos mínimos" observados. Substituindo $a$ na faixa de valores: $2550 \text{ nm} \le 680m \text{ nm} < 3060 \text{ nm}$ Dividindo por $680 \text{ nm}$: $\frac{2550}{680} \le m < \frac{3060}{680}$ $3.75 \le m < 4.5$ Como $m$ deve ser um número inteiro (representando a ordem do mínimo), o único valor possível para $m$ que satisfaz essa condição é $m=4$. Portanto, o mínimo para o qual $\sin(\theta) = \frac{3}{4}$ é o quarto mínimo ($m=4$). Agora, podemos calcular a largura da fenda $a$ usando a Equação 1 com $m=4$: $a = 680m \text{ nm}$ $a = 680 \times 4 \text{ nm}$ $a = 2720 \text{ nm}$ A largura da fenda é $2720 \text{ nm}$ ou $2.72 \times 10^{-6} \text{ m}$ ($2.72 \mu \text{m}$). The final answer is $\boxed{2720 \text{ nm}}$.
Está montando uma prova ou lista de exercícios?
Na plataforma da Teachy é possível gerar esses materiais automaticamente, sem perder horas buscando por questões 😉
Quem viu essa questão também gostou de...
Questão
Questão
Dificuldade Médio
Fonte:
ITA
Eletricidade: Problemas de Forças e Campos Elétricos
Dificuldade Médio
Questão
Questão
Dificuldade Médio
Fonte:
UNICAMP (TODOS OS ANOS)
Impulso e Quantidade de Movimento: Colisões em uma Dimensão • 'EM13CNT306'
Dificuldade Médio
Questão
Questão
Dificuldade Médio
Fonte:
SEMSP_PROVA_SEMESTRAL_SP
Astronomia: Fases da Lua • 'EF09CI15'
Dificuldade Médio
Questão
Questão
Dificuldade Médio
Fonte:
ITA
Eletricidade: Circuitos Elétricos • 'EM13CNT308'
Dificuldade Médio
Faça parte de uma comunidade de professores direto no seu WhatsApp
Conecte-se com outros professores, receba e compartilhe materiais, dicas, treinamentos, e muito mais!
2025 - Todos os direitos reservados