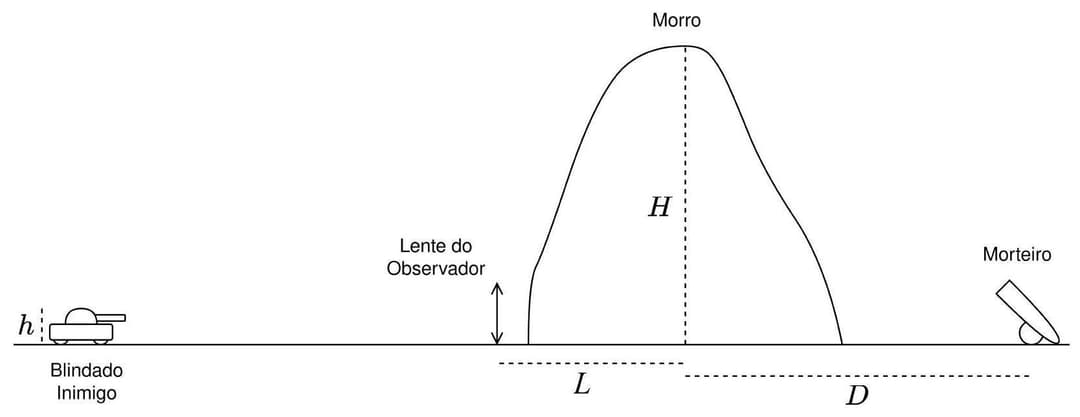
A resolução do problema envolve a análise de movimento de projéteis e óptica geométrica. --- **a) Distância horizontal $D$ do pico do morro onde o morteiro deve ser posicionado.** Para que o projétil atinja seu ponto máximo de trajetória (altura $H$) exatamente no pico do morro, podemos usar as equações do movimento de projéteis. A altura máxima $H$ é atingida quando a componente vertical da velocidade ($v_y$) é zero. A relação entre a velocidade inicial vertical ($v_{0y}$), a altura máxima ($H$) e a aceleração da gravidade ($g$) é dada por: $v_y^2 = v_{0y}^2 - 2gH$ No ponto de altura máxima, $v_y = 0$, então: $0 = v_{0y}^2 - 2gH \implies v_{0y}^2 = 2gH$ Substituindo os valores: $v_{0y}^2 = 2 \times 10 \mathrm{~m/s^2} \times 320 \mathrm{~m} = 6400 \mathrm{~m^2/s^2}$ $v_{0y} = \sqrt{6400} = 80 \mathrm{~m/s}$ O tempo ($t_{subida}$) que o projétil leva para atingir a altura máxima é: $v_y = v_{0y} - gt_{subida}$ $0 = 80 \mathrm{~m/s} - 10 \mathrm{~m/s^2} \times t_{subida}$ $t_{subida} = \frac{80 \mathrm{~m/s}}{10 \mathrm{~m/s^2}} = 8 \mathrm{~s}$ A velocidade inicial do projétil ($v_0$) é a resultante das componentes horizontal ($v_{0x}$) e vertical ($v_{0y}$): $v_0^2 = v_{0x}^2 + v_{0y}^2$ $100^2 = v_{0x}^2 + 80^2$ $10000 = v_{0x}^2 + 6400$ $v_{0x}^2 = 10000 - 6400 = 3600 \mathrm{~m^2/s^2}$ $v_{0x} = \sqrt{3600} = 60 \mathrm{~m/s}$ A distância horizontal $D$ do pico do morro (que é onde atinge a altura máxima) a partir do ponto de disparo (morteiro) é dada por: $D = v_{0x} \times t_{subida}$ $D = 60 \mathrm{~m/s} \times 8 \mathrm{~s} = 480 \mathrm{~m}$ --- **b) Distâncias entre o blindado e a lente nos momentos das duas medidas.** Usaremos a equação das lentes delgadas e a fórmula da ampliação. A ampliação $M$ é dada por: $M = \frac{i}{h} = -\frac{p'}{p}$, onde $i$ é o tamanho da imagem, $h$ é o tamanho do objeto, $p'$ é a distância da imagem à lente e $p$ é a distância do objeto à lente. Como a imagem é invertida, o sinal da ampliação é negativo. O problema fornece o "tamanho da imagem invertida", que é o módulo de $i$. Assim, podemos usar $|M| = \frac{|i|}{h} = \frac{p'}{p}$. Daqui, $p' = p \frac{|i|}{h}$. A equação das lentes delgadas é: $\frac{1}{f} = \frac{1}{p} + \frac{1}{p'}$. Substituindo $p'$: $\frac{1}{f} = \frac{1}{p} + \frac{1}{p \frac{|i|}{h}} = \frac{1}{p} \left(1 + \frac{h}{|i|}\right)$ Portanto, a distância do objeto $p$ é: $p = f \left(1 + \frac{h}{|i|}\right)$ * **Para a primeira medida:** $f = 50 \mathrm{~m}$, $h = 2.7 \mathrm{~m}$, $i_1 = 5.40 \mathrm{~cm} = 0.054 \mathrm{~m}$. $p_1 = 50 \mathrm{~m} \times \left(1 + \frac{2.7 \mathrm{~m}}{0.054 \mathrm{~m}}\right)$ $p_1 = 50 \mathrm{~m} \times (1 + 50) = 50 \mathrm{~m} \times 51 = 2550 \mathrm{~m}$ * **Para a segunda medida:** $f = 50 \mathrm{~m}$, $h = 2.7 \mathrm{~m}$, $i_2 = 6.75 \mathrm{~cm} = 0.0675 \mathrm{~m}$. $p_2 = 50 \mathrm{~m} \times \left(1 + \frac{2.7 \mathrm{~m}}{0.0675 \mathrm{~m}}\right)$ $p_2 = 50 \mathrm{~m} \times (1 + 40) = 50 \mathrm{~m} \times 41 = 2050 \mathrm{~m}$ As distâncias do blindado à lente são $p_1 = 2550 \mathrm{~m}$ e $p_2 = 2050 \mathrm{~m}$. --- **c) Velocidade do blindado.** O blindado se desloca com velocidade constante em direção à lente. A distância percorrida pelo blindado entre as duas medidas é $\Delta p = p_1 - p_2$. $\Delta p = 2550 \mathrm{~m} - 2050 \mathrm{~m} = 500 \mathrm{~m}$ O intervalo de tempo entre as medidas é $\Delta t = 25 \mathrm{~s}$. A velocidade do blindado ($v_{blindado}$) é: $v_{blindado} = \frac{\Delta p}{\Delta t} = \frac{500 \mathrm{~m}}{25 \mathrm{~s}} = 20 \mathrm{~m/s}$ --- **d) Intervalo de tempo depois da segunda medida de imagem para que o disparo seja realizado e possa atingir o blindado.** Primeiro, vamos determinar a posição alvo do blindado em relação à lente no momento do impacto. O morteiro está a uma distância $D = 480 \mathrm{~m}$ do pico do morro. O projétil atinge seu ponto máximo no pico e continuará sua trajetória até atingir o solo (ou a mesma altura de disparo). O alcance horizontal total do projétil será $R = 2D$. $R = 2 \times 480 \mathrm{~m} = 960 \mathrm{~m}$. O tempo total de voo do projétil ($t_{voo}$) é o dobro do tempo de subida: $t_{voo} = 2 \times t_{subida} = 2 \times 8 \mathrm{~s} = 16 \mathrm{~s}$. Vamos definir um sistema de coordenadas onde o morteiro está na origem ($x=0$). O pico do morro está em $x_P = D = 480 \mathrm{~m}$. A lente está a uma distância $L = 110 \mathrm{~m}$ do pico. A figura indica que a lente está além do pico em relação ao morteiro. Então, a posição da lente é $x_L = x_P + L = 480 \mathrm{~m} + 110 \mathrm{~m} = 590 \mathrm{~m}$. O blindado deve ser atingido na posição $x_{impacto} = R = 960 \mathrm{~m}$ (a partir do morteiro). A distância do blindado à lente no momento do impacto ($p_{alvo}$) é: $p_{alvo} = x_{impacto} - x_L = 960 \mathrm{~m} - 590 \mathrm{~m} = 370 \mathrm{~m}$. No momento da segunda medida, o blindado está a uma distância $p_2 = 2050 \mathrm{~m}$ da lente. Seja $t_{disparo}$ o tempo, após a segunda medida, em que o morteiro é disparado. Quando o morteiro é disparado, o blindado já percorreu uma distância $v_{blindado} \times t_{disparo}$ em direção à lente. Sua posição em relação à lente no momento do disparo é $p_{disparo} = p_2 - v_{blindado} \times t_{disparo}$. Após o disparo, o projétil leva $t_{voo}$ segundos para atingir o blindado. Durante esse tempo, o blindado continua se movendo. A distância percorrida pelo blindado durante o tempo de voo do projétil é $v_{blindado} \times t_{voo}$. A distância do blindado à lente no momento do impacto ($p_{impacto}$) será: $p_{impacto} = p_{disparo} - v_{blindado} \times t_{voo}$ Para o sucesso do impacto, $p_{impacto}$ deve ser igual a $p_{alvo}$: $p_{alvo} = (p_2 - v_{blindado} \times t_{disparo}) - v_{blindado} \times t_{voo}$ $p_{alvo} = p_2 - v_{blindado} \times (t_{disparo} + t_{voo})$ Podemos rearranjar a equação para encontrar $t_{disparo}$: $v_{blindado} \times (t_{disparo} + t_{voo}) = p_2 - p_{alvo}$ $t_{disparo} + t_{voo} = \frac{p_2 - p_{alvo}}{v_{blindado}}$ $t_{disparo} = \frac{p_2 - p_{alvo}}{v_{blindado}} - t_{voo}$ Substituindo os valores: $t_{disparo} = \frac{2050 \mathrm{~m} - 370 \mathrm{~m}}{20 \mathrm{~m/s}} - 16 \mathrm{~s}$ $t_{disparo} = \frac{1680 \mathrm{~m}}{20 \mathrm{~m/s}} - 16 \mathrm{~s}$ $t_{disparo} = 84 \mathrm{~s} - 16 \mathrm{~s}$ $t_{disparo} = 68 \mathrm{~s}$ --- **Resumo das respostas:** a) A distância horizontal $D$ do pico do morro onde o morteiro deve ser posicionado é $\boxed{480 \mathrm{~m}}$. b) As distâncias entre o blindado e a lente nos momentos das duas medidas são $\boxed{2550 \mathrm{~m}}$ e $\boxed{2050 \mathrm{~m}}$. c) A velocidade do blindado é $\boxed{20 \mathrm{~m/s}}$. d) O intervalo de tempo depois da segunda medida de imagem para que o disparo seja realizado é $\boxed{68 \mathrm{~s}}$.