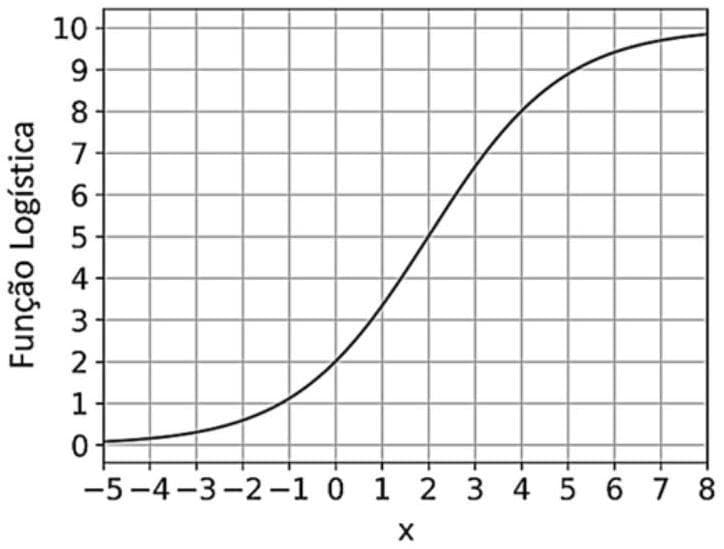
a) Seja \(y=\frac{L}{1+2^{-k\left(x-x_{0}\right)}}\). Note que \(y>0\). Agora, para determinar a função inversa \(x=f^{-1}(y)\), vamos isolar \(x\) nessa equação: \(y \cdot\left(1+2^{-k\left(x-x_{0}\right)}\right)=L\) Dividindo por \(y\) e subtraindo 1 dos dois lados, temos \(2^{-k\left(x-x_{0}\right)}=\frac{L-y}{y}\). A ideia agora é calcular o logaritmo na base 2 em ambos os lados da igualdade, mas, para isso, temos que garantir que ambos são positivos. O lado esquerdo é positivo, pois é uma potência de 2 . Para o lado direito, precisamos supor que \(\frac{L-y}{y}>0\). Como \(y>0\), será preciso que \(L-y>0\), o que é equivalente a \(y<L\). Determinamos, portanto, o domínio da função inversa: \(0<y<L\). Dentro dessa condição, podemos agora aplicar o logaritmo e transformar a equação anterior em \(-k\left(x-x_{0}\right)=\log _{2}\left(\frac{L-y}{y}\right)\), o que passando o sinal para o lado direito, dividindo por \(k\) e somando \(x_{0}\) em ambos os lados resulta em \(x=x_{0}+\frac{1}{k} \cdot \log _{2}\left(\frac{y}{L-y}\right)\). b) Note que se \(x=x_{0}\) então \(y=f\left(x_{0}\right)=\frac{L}{1+2^{0}}=\frac{L}{2}=\frac{10}{2}=5\) Pelo gráfico, vemos que \(f(2)=5\), portanto \(x_{0}=2\) e temos \(y=\frac{10}{1+2^{-k(x-2)}}\) Pelo gráfico, obtemos que \(f(0)=2\), portanto \(2=\frac{10}{1+2^{-k(-2)}}\) ou \(2\left(1+2^{2 k}\right)=10\), o que nos dá \(k=1\).