Questão sobre Termoquímica: Energia Livre de Gibbs
Fonte: IME-2FASE
Disciplina Química
Química
BNCC 'EM13CNT102'
'EM13CNT102'
Assunto Termoquímica: Energia Livre de Gibbs
Termoquímica: Energia Livre de Gibbs
Dificuldade Médio
Médio
(IME-2FASE 2024) - Questão Médio de Química
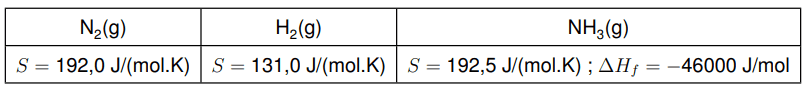
Gabarito
A seguir, apresenta-se a solução detalhada para cada uma das partes da questão: **a) Cálculo do valor de $\Delta G_{r}(T)$** Primeiramente, é necessário escrever a equação balanceada da reação de produção de amônia: $\mathrm{N}_{2}(\mathrm{~g}) + 3\mathrm{H}_{2}(\mathrm{~g}) \rightleftharpoons 2\mathrm{NH}_{3}(\mathrm{~g})$ Em seguida, calculamos a variação da entalpia padrão da reação ($\Delta H_r$) e a variação da entropia padrão da reação ($\Delta S_r$) utilizando os dados fornecidos e considerando que as entalpias de formação de substâncias elementares são zero. 1. **Cálculo de $\Delta H_r$:** $\Delta H_r = \sum n_p \Delta H_f(\text{produtos}) - \sum n_r \Delta H_f(\text{reagentes})$ $\Delta H_f(\mathrm{N}_{2}(\mathrm{~g})) = 0 \mathrm{~J/mol}$ $\Delta H_f(\mathrm{H}_{2}(\mathrm{~g})) = 0 \mathrm{~J/mol}$ $\Delta H_f(\mathrm{NH}_{3}(\mathrm{~g})) = -46000 \mathrm{~J/mol}$ $\Delta H_r = [2 \times (-46000 \mathrm{~J/mol})] - [1 \times (0 \mathrm{~J/mol}) + 3 \times (0 \mathrm{~J/mol})]$ $\Delta H_r = -92000 \mathrm{~J/mol}$ 2. **Cálculo de $\Delta S_r$:** $\Delta S_r = \sum n_p S(\text{produtos}) - \sum n_r S(\text{reagentes})$ $S(\mathrm{N}_{2}(\mathrm{~g})) = 192.0 \mathrm{~J/(mol \cdot K)}$ $S(\mathrm{H}_{2}(\mathrm{~g})) = 131.0 \mathrm{~J/(mol \cdot K)}$ $S(\mathrm{NH}_{3}(\mathrm{~g})) = 192.5 \mathrm{~J/(mol \cdot K)}$ $\Delta S_r = [2 \times (192.5 \mathrm{~J/(mol \cdot K)})] - [1 \times (192.0 \mathrm{~J/(mol \cdot K)}) + 3 \times (131.0 \mathrm{~J/(mol \cdot K)})]$ $\Delta S_r = 385.0 \mathrm{~J/(mol \cdot K)} - [192.0 \mathrm{~J/(mol \cdot K)} + 393.0 \mathrm{~J/(mol \cdot K)}]$ $\Delta S_r = 385.0 \mathrm{~J/(mol \cdot K)} - 585.0 \mathrm{~J/(mol \cdot K)}$ $\Delta S_r = -200.0 \mathrm{~J/(mol \cdot K)}$ 3. **Cálculo da temperatura ($T_0$) em que a reação deixa de ser espontânea:** Uma reação deixa de ser espontânea quando $\Delta G_r = 0$. Utilizando a equação de Gibbs-Helmholtz: $\Delta G_r = \Delta H_r - T \Delta S_r$ $0 = \Delta H_r - T_0 \Delta S_r$ $T_0 = \frac{\Delta H_r}{\Delta S_r}$ $T_0 = \frac{-92000 \mathrm{~J/mol}}{-200.0 \mathrm{~J/(mol \cdot K)}}$ $T_0 = 460 \mathrm{~K}$ 4. **Cálculo da temperatura de operação ($T$):** O enunciado afirma que a reação ocorre em uma temperatura $T$ que é $113^{\circ} \mathrm{C}$ maior do que $T_0$. Uma variação de temperatura em graus Celsius é equivalente à mesma variação em Kelvin. $T = T_0 + 113 \mathrm{~K}$ $T = 460 \mathrm{~K} + 113 \mathrm{~K}$ $T = 573 \mathrm{~K}$ 5. **Cálculo de $\Delta G_r(T)$ na temperatura de operação:** $\Delta G_r(T) = \Delta H_r - T \Delta S_r$ $\Delta G_r(T) = -92000 \mathrm{~J/mol} - (573 \mathrm{~K}) \times (-200.0 \mathrm{~J/(mol \cdot K)})$ $\Delta G_r(T) = -92000 \mathrm{~J/mol} + 114600 \mathrm{~J/mol}$ $\Delta G_r(T) = 22600 \mathrm{~J/mol}$ **b) Determinação da constante de equilíbrio ($K_{eq}$)** A relação entre a energia livre de Gibbs padrão da reação ($\Delta G_r$) e a constante de equilíbrio ($K_{eq}$) é dada pela equação: $\Delta G_r = -RT \ln K_{eq}$ No item (a), calculamos $\Delta G_r(T) = 22600 \mathrm{~J/mol}$. Como $R$ (constante dos gases ideais) e $T$ (temperatura em Kelvin) são valores positivos, podemos analisar o sinal de $K_{eq}$ a partir do sinal de $\Delta G_r$: * Se $\Delta G_r < 0$, então $\ln K_{eq} > 0$, o que implica $K_{eq} > 1$. * Se $\Delta G_r = 0$, então $\ln K_{eq} = 0$, o que implica $K_{eq} = 1$. * Se $\Delta G_r > 0$, então $\ln K_{eq} < 0$, o que implica $K_{eq} < 1$. Como $\Delta G_r(T) = 22600 \mathrm{~J/mol}$ é um valor positivo ($\Delta G_r > 0$), a constante de equilíbrio da reação de produção de amônia será **$K_{eq} < 1$**. **c) Justificativa sobre a pressão para maior produção de $\mathrm{NH}_{3}(\mathrm{~g})$ no equilíbrio** Para determinar em qual pressão haverá maior produção de $\mathrm{NH}_{3}(\mathrm{~g})$ no equilíbrio, aplicamos o Princípio de Le Chatelier. A reação é: $\mathrm{N}_{2}(\mathrm{~g}) + 3\mathrm{H}_{2}(\mathrm{~g}) \rightleftharpoons 2\mathrm{NH}_{3}(\mathrm{~g})$ Vamos analisar o número de mols de gases em cada lado da equação: * **Reagentes:** $1 \mathrm{~mol}$ de $\mathrm{N}_{2}(\mathrm{~g}) + 3 \mathrm{~mol}$ de $\mathrm{H}_{2}(\mathrm{~g}) = 4 \mathrm{~mol}$ de gás * **Produtos:** $2 \mathrm{~mol}$ de $\mathrm{NH}_{3}(\mathrm{~g})$ Observa-se que a reação direta (produção de amônia) leva a uma diminuição no número total de mols de gás (de 4 mols para 2 mols). O Princípio de Le Chatelier estabelece que, se uma perturbação externa (como mudança de pressão) é aplicada a um sistema em equilíbrio, o sistema se deslocará de forma a minimizar essa perturbação. No caso de um aumento de pressão, o equilíbrio se deslocará para o lado da reação que produz o menor número de mols de gás, a fim de aliviar essa pressão. Como a formação de amônia (sentido direto) resulta em uma redução do número de mols de gás, um aumento de pressão favorecerá a produção de $\mathrm{NH}_{3}(\mathrm{~g})$. Portanto, entre $P=1 \mathrm{~atm}$ e $P=200 \mathrm{~atm}$, haverá **maior produção de $\mathrm{NH}_{3}(\mathrm{~g})$ no equilíbrio a $P=200 \mathrm{~atm}$**.
Está montando uma prova ou lista de exercícios?
Na plataforma da Teachy é possível gerar esses materiais automaticamente, sem perder horas buscando por questões 😉
Quem viu essa questão também gostou de...
Questão
Questão
Dificuldade Fácil
Fonte:
Teachy
Reações: Balanceamento • 'EM13CNT101'
Dificuldade Fácil
Questão
Questão
Dificuldade Fácil
Fonte:
UFTM
Reações: Balanceamento de Equação Redox • 'EM13CNT101'
Dificuldade Fácil
Questão
Questão
Dificuldade Difícil
Fonte:
Teachy
Leis ponderais: Proust • 'EM13CNT101'
Dificuldade Difícil
Questão
Questão
Dificuldade Médio
Fonte:
Teachy
Soluções: Introdução
Dificuldade Médio
Faça parte de uma comunidade de professores direto no seu WhatsApp
Conecte-se com outros professores, receba e compartilhe materiais, dicas, treinamentos, e muito mais!
2025 - Todos os direitos reservados