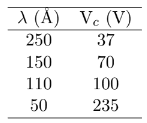
(a) **Determinação da Função Trabalho da Placa Metálica** A equação do efeito fotoelétrico relaciona a energia cinética máxima dos fotoelétrons ($E_k^{max}$), a frequência da radiação incidente ($f$) e a função trabalho ($\phi$) do material: $E_k^{max} = hf - \phi$ Sabemos que a energia cinética máxima dos elétrons é dada por $E_k^{max} = eV_c$, onde $e$ é a carga elementar e $V_c$ é o potencial de corte. Além disso, a frequência da radiação é $f = c/\lambda$, onde $c$ é a velocidade da luz e $\lambda$ é o comprimento de onda. Substituindo na equação, obtemos: $eV_c = \frac{hc}{\lambda} - \phi$ Podemos reescrever esta equação na forma de uma reta $y = mx + b$: $V_c = \left(\frac{hc}{e}\right) \frac{1}{\lambda} - \frac{\phi}{e}$ Onde $y = V_c$, $x = 1/\lambda$, o coeficiente angular $m = \frac{hc}{e}$ e o coeficiente linear $b = -\frac{\phi}{e}$. Vamos utilizar dois pontos da tabela para determinar o coeficiente angular $m$ e, posteriormente, o coeficiente linear $b$. Escolheremos os pontos $(\lambda_1, V_{c1}) = (250 \AA, 37 \mathrm{~V})$ e $(\lambda_2, V_{c2}) = (50 \AA, 235 \mathrm{~V})$. Primeiro, convertemos os comprimentos de onda para metros e calculamos seus inversos: $1/\lambda_1 = 1/(250 \times 10^{-10} \mathrm{~m}) = 4 \times 10^7 \mathrm{~m}^{-1}$ $1/\lambda_2 = 1/(50 \times 10^{-10} \mathrm{~m}) = 20 \times 10^7 \mathrm{~m}^{-1}$ Agora, calculamos o coeficiente angular ($m$): $m = \frac{\Delta V_c}{\Delta (1/\lambda)} = \frac{V_{c2} - V_{c1}}{(1/\lambda_2) - (1/\lambda_1)}$ $m = \frac{235 \mathrm{~V} - 37 \mathrm{~V}}{(20 \times 10^7 \mathrm{~m}^{-1}) - (4 \times 10^7 \mathrm{~m}^{-1})} = \frac{198 \mathrm{~V}}{16 \times 10^7 \mathrm{~m}^{-1}} = 12.375 \times 10^{-7} \mathrm{~V \cdot m}$ Este valor de $m$ corresponde a $\frac{hc}{e}$. Agora podemos usar um dos pontos e o valor de $m$ para encontrar $\frac{\phi}{e}$: $V_c = m \frac{1}{\lambda} - \frac{\phi}{e} \implies \frac{\phi}{e} = m \frac{1}{\lambda} - V_c$ Usando o primeiro ponto $(\lambda_1, V_{c1}) = (250 \AA, 37 \mathrm{~V})$: $\frac{\phi}{e} = (12.375 \times 10^{-7} \mathrm{~V \cdot m}) (4 \times 10^7 \mathrm{~m}^{-1}) - 37 \mathrm{~V}$ $\frac{\phi}{e} = 49.5 \mathrm{~V} - 37 \mathrm{~V} = 12.5 \mathrm{~V}$ Portanto, a função trabalho $\phi$ em elétron-volts (eV) é: $\phi = 12.5 \mathrm{~eV}$ (b) **Saltos Quânticos do Átomo de Hidrogênio Capazes de Emitir Fotoelétrons** Para que um fotoelétron seja emitido, a energia do fóton incidente ($E_p$) deve ser maior ou igual à função trabalho ($\phi$) da placa metálica. $E_p \ge \phi$ Do item (a), sabemos que $\phi = 12.5 \mathrm{~eV}$. A energia dos fótons emitidos por um átomo de hidrogênio durante uma transição de um nível de energia inicial $n_i$ para um nível final $n_f$ é dada por: $E_p = 13.6 \left( \frac{1}{n_f^2} - \frac{1}{n_i^2} \right) \mathrm{~eV}$, onde $n_i > n_f$. Vamos analisar as diferentes séries espectrais do hidrogênio: 1. **Série de Lyman ($n_f = 1$):** Nesta série, os elétrons caem para o nível fundamental ($n_f=1$). As energias dos fótons são: * $n_i = 2 \to n_f = 1$: $E_p = 13.6 (1/1^2 - 1/2^2) = 13.6 (3/4) = 10.2 \mathrm{~eV}$. Como $10.2 \mathrm{~eV} < 12.5 \mathrm{~eV}$, este salto *não* é capaz de emitir fotoelétrons. * $n_i = 3 \to n_f = 1$: $E_p = 13.6 (1/1^2 - 1/3^2) = 13.6 (8/9) \approx 12.09 \mathrm{~eV}$. Como $12.09 \mathrm{~eV} < 12.5 \mathrm{~eV}$, este salto *não* é capaz de emitir fotoelétrons. * $n_i = 4 \to n_f = 1$: $E_p = 13.6 (1/1^2 - 1/4^2) = 13.6 (15/16) = 12.75 \mathrm{~eV}$. Como $12.75 \mathrm{~eV} \ge 12.5 \mathrm{~eV}$, este salto *é* capaz de emitir fotoelétrons. * $n_i = 5 \to n_f = 1$: $E_p = 13.6 (1/1^2 - 1/5^2) = 13.6 (24/25) = 13.056 \mathrm{~eV}$. Como $13.056 \mathrm{~eV} \ge 12.5 \mathrm{~eV}$, este salto *é* capaz de emitir fotoelétrons. * Para $n_i \to \infty$: $E_p = 13.6 (1/1^2 - 0) = 13.6 \mathrm{~eV}$. Todos os saltos para $n_f=1$ com $n_i \ge 4$ terão energia maior ou igual a $12.75 \mathrm{~eV}$, sendo, portanto, capazes de causar a emissão fotoelétrica. 2. **Série de Balmer ($n_f = 2$):** Nesta série, os elétrons caem para o segundo nível de energia ($n_f=2$). A maior energia de fóton nesta série ocorre para $n_i \to \infty$: $E_p = 13.6 (1/2^2 - 0) = 13.6/4 = 3.4 \mathrm{~eV}$. Como $3.4 \mathrm{~eV} < 12.5 \mathrm{~eV}$, nenhum salto da série de Balmer é capaz de emitir fotoelétrons. 3. **Série de Paschen ($n_f = 3$) e séries superiores:** As energias dos fótons para $n_f \ge 3$ são ainda menores que as da série de Balmer. Por exemplo, a maior energia para a série de Paschen ($n_i \to \infty, n_f=3$) é $13.6/9 \approx 1.51 \mathrm{~eV}$, que é muito menor que a função trabalho. **Conclusão:** Apenas os saltos quânticos da série de Lyman, onde os elétrons do átomo de hidrogênio caem para o nível fundamental ($n_f=1$) a partir de um nível de energia inicial $n_i$ igual ou superior a 4, são capazes de emitir fotoelétrons da placa metálica. Esses saltos são: * $n_i = 4 \to n_f = 1$ * $n_i = 5 \to n_f = 1$ * $n_i = 6 \to n_f = 1$ * e assim por diante, para todos os $n_i \ge 4$ até $n_i = \infty$.