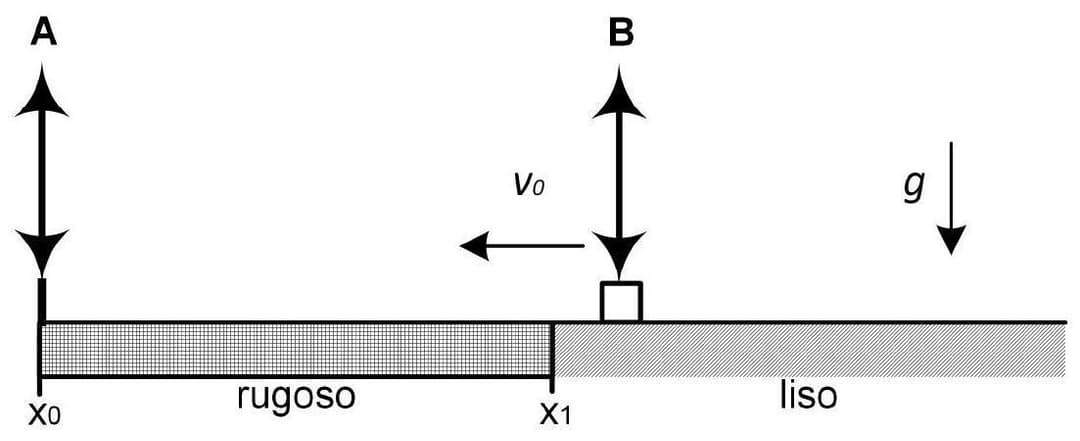
Para resolver este problema, precisamos analisar as condições ópticas e cinemáticas do sistema. **1. Análise do Sistema Óptico:** * **Objeto Distante:** O objeto está muito distante à esquerda da lente A, o que significa que ele está no infinito (\(p_A = -\infty\)). * **Imagem Formada pela Lente A (\(I_A\)):** Como a lente A é convergente e o objeto está no infinito, a imagem \(I_A\) será real, invertida e se formará no foco da lente A, à sua direita. * Distância focal da lente A: \(f_A = f\). * A posição da lente A é \(x_0\). * A posição da imagem \(I_A\) é \(x_{I_A} = x_0 + f\). * **\(I_A\) como Objeto para a Lente B:** A imagem \(I_A\) atua como objeto para a lente B. * Distância focal da lente B: \(f_B = 2f\). * Seja \(x_B\) a posição da lente B. Como o objeto está à esquerda da lente A e a lente B se move para a esquerda de A, a lente A está à esquerda da lente B na configuração usual de formação de imagem. Assim, \(x_B > x_0\). * A distância do objeto para a lente B (\(p_B\)) é a distância entre a lente B e a imagem \(I_A\). Para que \(I_A\) seja um objeto real para B, \(I_A\) deve estar à esquerda de B. Portanto, \(p_B = x_B - x_{I_A} = x_B - (x_0 + f)\). * **Condição para Imagem Final Real:** O problema estabelece que o sistema não deve produzir uma imagem virtual. Para uma lente convergente, a imagem final (\(I_B\)) é real se o objeto real estiver localizado além do seu ponto focal. * Assim, para a lente B, a condição para a imagem \(I_B\) ser real é \(p_B \ge f_B\). * Substituindo os valores: \(x_B - (x_0 + f) \ge 2f\). * Simplificando: \(x_B - x_0 - f \ge 2f \implies x_B - x_0 \ge 3f\). * A distância entre as lentes é \(d = x_B - x_0\). Portanto, a condição é \(d \ge 3f\). * Se \(d = 3f\), a imagem \(I_B\) é formada no infinito, o que é considerado uma imagem real. Se \(d < 3f\), a imagem seria virtual. **2. Análise do Movimento do Bloco:** * **Movimento Inicial:** O bloco se move da direita para a esquerda com velocidade constante \(v_0\) até a posição \(x_1\). * **Movimento no Piso Rugoso:** A partir de \(x_1\), o piso se torna rugoso, e o bloco sofre uma força de atrito cinético. * Força de atrito: \(F_{at} = \mu N = \mu mg\). * Aceleração (desaceleração): \(a = -F_{at}/m = -\mu g\). A aceleração é constante e aponta para a direita (sentido oposto ao movimento). * **Parada do Bloco:** O bloco para em uma posição final \(x_{parada}\). O movimento ocorre de \(x_1\) para a esquerda, então \(x_{parada} < x_1\). * **Equação Cinemática:** Usando a equação de Torricelli: \(v_f^2 = v_i^2 + 2a\Delta x\). * \(v_f = 0\) (velocidade final é zero, o bloco para). * \(v_i = v_0\) (velocidade inicial na zona rugosa). * \(a = -\mu g\). * \(\Delta x = x_{parada} - x_1\) (deslocamento, que é negativo). * \(0^2 = v_0^2 + 2(-\mu g)(x_{parada} - x_1)\). * \(v_0^2 = 2\mu g (x_1 - x_{parada})\). **3. Combinando as Condições:** Queremos determinar o maior valor de \(v_0\) para o qual o bloco entra em repouso sem que o sistema produza uma imagem virtual. Isso significa que, na posição final de parada \(x_{parada}\), a condição óptica deve ser satisfeita. * A posição da lente B quando o bloco para é \(x_{parada}\). * A condição óptica é: \(x_{parada} \ge x_0 + 3f\). Da equação cinemática, para maximizar \(v_0\), precisamos maximizar o termo \((x_1 - x_{parada})\). Isso implica que \(x_{parada}\) deve ser o menor possível. A condição óptica \(x_{parada} \ge x_0 + 3f\) nos dá um limite inferior para \(x_{parada}\). O menor valor possível que \(x_{parada}\) pode assumir é quando ele está no limite da condição, ou seja: \(x_{parada, mín} = x_0 + 3f\). Substituindo este valor mínimo de \(x_{parada}\) na equação de \(v_0\): \(v_0^2_{máx} = 2\mu g (x_1 - (x_0 + 3f))\). \(v_{0,máx} = \sqrt{2\mu g (x_1 - x_0 - 3f)}\). **4. Condição de Existência:** Para que \(v_{0,máx}\) seja um valor real, o termo dentro da raiz quadrada deve ser não negativo: \(x_1 - x_0 - 3f \ge 0 \implies x_1 \ge x_0 + 3f\). Isso significa que a posição onde o bloco começa a desacelerar (\(x_1\)) deve ser tal que a imagem formada já seja real (ou no infinito). Se \(x_1 < x_0 + 3f\), a imagem seria virtual já no início da desaceleração, e não haveria nenhum \(v_0\) que satisfizesse a condição. A solução final para o maior valor de \(v_0\) é: \(\boxed{v_{0,máx} = \sqrt{2\mu g (x_1 - x_0 - 3f)}}\)