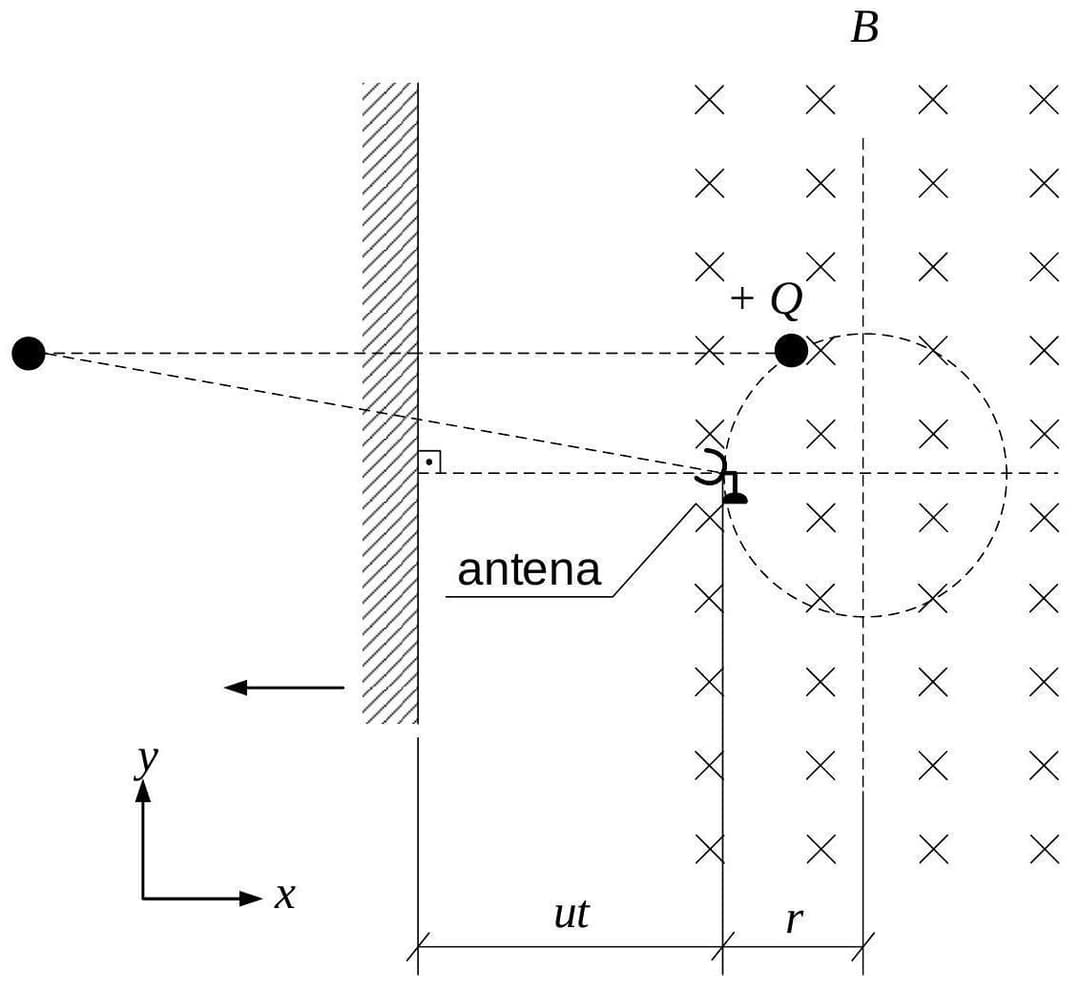
Apresentamos a solução detalhada para cada item do problema. **1. Definição do Sistema de Coordenadas e Variáveis:** * Adotamos um sistema de coordenadas cartesiano com a origem $(0,0)$ no centro da trajetória circular da partícula. * A antena está fixa no ponto mais à esquerda da trajetória, ou seja, na posição $A = (-r, 0)$. * A partícula carregada ($+Q$, massa $m$) move-se em uma trajetória circular de raio $r$. * No instante $t=0$, a partícula está no ponto mais à direita da trajetória, $P(0) = (r, 0)$. * A velocidade angular da partícula, $\omega_p$, é determinada pela força magnética que atua como força centrípeta: $QvB = mv^2/r \Rightarrow v = QBr/m$. Portanto, $\omega_p = v/r = QB/m$. * Assumiremos que a partícula se move no sentido horário. Esta escolha é consistente com a convenção comum para uma carga positiva em um campo magnético (por exemplo, se o campo magnético estiver saindo da página no plano XY). * Assim, a posição da partícula em função do tempo é: $x_p(t) = r \cos(\omega_p t)$ $y_p(t) = -r \sin(\omega_p t)$ * O espelho plano se move para a esquerda com velocidade constante $u$. * No instante $t=0$, o espelho parte da posição da antena, ou seja, $x_M(0) = -r$. * A posição do espelho em função do tempo é: $x_M(t) = -r - ut$ **2. Princípio da Formação da Imagem em um Espelho Plano:** Para um objeto em $(x_p, y_p)$ e um espelho plano perpendicular ao eixo x na posição $x_M$, a imagem $(x_I, y_I)$ é dada por: $x_I = x_M - (x_p - x_M) = 2x_M - x_p$ $y_I = y_p$ --- ### a) As componentes $x$ e $y$ da posição da imagem da partícula em relação à antena Primeiro, calculamos a posição da imagem $(x_I, y_I)$ no sistema de coordenadas global: $x_I(t) = 2x_M(t) - x_p(t) = 2(-r - ut) - r \cos(\omega_p t)$ $x_I(t) = -2r - 2ut - r \cos(\omega_p t)$ $y_I(t) = y_p(t) = -r \sin(\omega_p t)$ A posição da antena é $A = (-r, 0)$. A posição da imagem em relação à antena, $\vec{R}_{IA}(t) = (x_{IA}(t), y_{IA}(t))$, é dada por $\vec{R}_{IA}(t) = \vec{I}(t) - \vec{A}$. $x_{IA}(t) = x_I(t) - (-r) = (-2r - 2ut - r \cos(\omega_p t)) + r$ $x_{IA}(t) = -r - 2ut - r \cos(\omega_p t)$ $x_{IA}(t) = -r(1 + \cos(\omega_p t)) - 2ut$ $y_{IA}(t) = y_I(t) - 0 = -r \sin(\omega_p t)$ Substituindo $\omega_p = QB/m$: $\boxed{x_{IA}(t) = -r\left(1 + \cos\left(\frac{QBt}{m}\right)\right) - 2ut}$ $\boxed{y_{IA}(t) = -r\sin\left(\frac{QBt}{m}\right)}$ --- ### b) As componentes $x$ e $y$ da velocidade da imagem da partícula A velocidade da imagem é a derivada temporal de sua posição no sistema de coordenadas global, $\vec{v}_I(t) = (\frac{dx_I}{dt}, \frac{dy_I}{dt})$. Como a antena está fixa, a velocidade da imagem em relação à antena é a mesma que a velocidade da imagem em relação ao sistema de coordenadas global. $v_{Ix}(t) = \frac{d}{dt}(-2r - 2ut - r \cos(\omega_p t))$ $v_{Ix}(t) = 0 - 2u - r(-\sin(\omega_p t))\omega_p$ $v_{Ix}(t) = -2u + r\omega_p \sin(\omega_p t)$ $v_{Iy}(t) = \frac{d}{dt}(-r \sin(\omega_p t))$ $v_{Iy}(t) = -r\omega_p \cos(\omega_p t)$ Substituindo $\omega_p = QB/m$: $\boxed{v_{Ix}(t) = -2u + r\left(\frac{QB}{m}\right)\sin\left(\frac{QBt}{m}\right)}$ $\boxed{v_{Iy}(t) = -r\left(\frac{QB}{m}\right)\cos\left(\frac{QBt}{m}\right)}$ --- ### c) A velocidade angular da antena, a partir dos resultados obtidos nos itens anteriores A antena acompanha a imagem, o que significa que o vetor posição da imagem em relação à antena, $\vec{R}_{IA}(t) = (x_{IA}(t), y_{IA}(t))$, define a orientação da antena. A velocidade angular da antena, $\omega_A(t)$, é a derivada temporal do ângulo $\theta_A(t)$ que $\vec{R}_{IA}(t)$ faz com o eixo x. A fórmula para a velocidade angular de um vetor em coordenadas polares é: $\omega_A(t) = \frac{x_{IA}(t) v_{IA,y}(t) - y_{IA}(t) v_{IA,x}(t)}{x_{IA}(t)^2 + y_{IA}(t)^2}$ Onde $v_{IA,x}(t) = \frac{dx_{IA}}{dt}$ e $v_{IA,y}(t) = \frac{dy_{IA}}{dt}$. Usando os resultados do item (a) e (b), notamos que $v_{IA,x} = v_{Ix}$ e $v_{IA,y} = v_{Iy}$. Vamos calcular o numerador ($N$) e o denominador ($D$): **Numerador ($N$):** $N = x_{IA}(t) v_{IA,y}(t) - y_{IA}(t) v_{IA,x}(t)$ $N = \left(-r(1 + \cos(\omega_p t)) - 2ut\right) \left(-r\omega_p \cos(\omega_p t)\right) - \left(-r \sin(\omega_p t)\right) \left(-2u + r\omega_p \sin(\omega_p t)\right)$ Expandindo o primeiro termo: $(-r(1 + \cos(\omega_p t)) - 2ut)(-r\omega_p \cos(\omega_p t)) = r^2\omega_p(1 + \cos(\omega_p t))\cos(\omega_p t) + 2ut r\omega_p \cos(\omega_p t)$ $= r^2\omega_p(\cos(\omega_p t) + \cos^2(\omega_p t)) + 2ut r\omega_p \cos(\omega_p t)$ Expandindo o segundo termo: $-(-r \sin(\omega_p t))(-2u + r\omega_p \sin(\omega_p t)) = (r \sin(\omega_p t))(-2u + r\omega_p \sin(\omega_p t))$ $= -2ur \sin(\omega_p t) + r^2\omega_p \sin^2(\omega_p t)$ Somando os dois termos para obter $N$: $N = r^2\omega_p\cos(\omega_p t) + r^2\omega_p\cos^2(\omega_p t) + 2ut r\omega_p \cos(\omega_p t) - 2ur \sin(\omega_p t) + r^2\omega_p \sin^2(\omega_p t)$ Agrupando os termos com $r^2\omega_p$: $N = r^2\omega_p(\cos(\omega_p t) + \cos^2(\omega_p t) + \sin^2(\omega_p t)) + 2ut r\omega_p \cos(\omega_p t) - 2ur \sin(\omega_p t)$ Usando a identidade trigonométrica $\cos^2\theta + \sin^2\theta = 1$: $N = r^2\omega_p(1 + \cos(\omega_p t)) + 2ut r\omega_p \cos(\omega_p t) - 2ur \sin(\omega_p t)$ **Denominador ($D$):** $D = x_{IA}(t)^2 + y_{IA}(t)^2$ $D = \left(-r(1 + \cos(\omega_p t)) - 2ut\right)^2 + \left(-r \sin(\omega_p t)\right)^2$ $D = \left(r(1 + \cos(\omega_p t)) + 2ut\right)^2 + r^2 \sin^2(\omega_p t)$ $D = r^2(1 + \cos(\omega_p t))^2 + 2 \cdot r(1 + \cos(\omega_p t)) \cdot (2ut) + (2ut)^2 + r^2 \sin^2(\omega_p t)$ $D = r^2(1 + 2\cos(\omega_p t) + \cos^2(\omega_p t)) + 4ut r(1 + \cos(\omega_p t)) + 4u^2t^2 + r^2 \sin^2(\omega_p t)$ $D = r^2(1 + 2\cos(\omega_p t) + \cos^2(\omega_p t) + \sin^2(\omega_p t)) + 4ut r(1 + \cos(\omega_p t)) + 4u^2t^2$ $D = r^2(2 + 2\cos(\omega_p t)) + 4ut r(1 + \cos(\omega_p t)) + 4u^2t^2$ $D = 2r^2(1 + \cos(\omega_p t)) + 4ut r(1 + \cos(\omega_p t)) + 4u^2t^2$ Podemos fatorar $2r(1 + \cos(\omega_p t))$ dos dois primeiros termos: $D = 2r(1 + \cos(\omega_p t))(r + 2ut) + 4u^2t^2$ Finalmente, a velocidade angular da antena é $\omega_A(t) = N/D$: $\boxed{\omega_A(t) = \frac{r^2\omega_p(1 + \cos(\omega_p t)) + 2ut r\omega_p \cos(\omega_p t) - 2ur \sin(\omega_p t)}{2r(r + 2ut)(1 + \cos(\omega_p t)) + 4u^2t^2}}$ Onde $\omega_p = QB/m$.