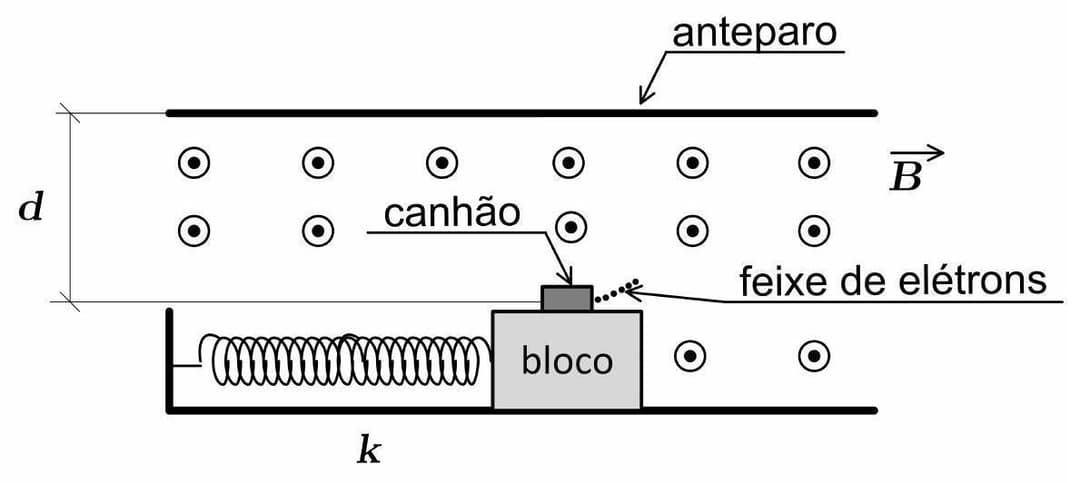
A resolução das diferentes alíneas deste problema exige uma interpretação cuidadosa do enunciado, que contém algumas nuances que podem levar a inconsistências se não forem assumidas certas condições. Adotaremos as interpretações mais diretas e comuns em problemas de física, esclarecendo as premissas quando necessário. --- **a) A amplitude de oscilação do bloco para que o experimento seja viável, em função de $v, M$ e $k$.** Para que o experimento seja viável, os elétrons devem ser capazes de se mover em direção ao anteparo (ou realizar as trajetórias descritas). O canhão dispara elétrons com velocidade $v$ em relação a si mesmo. O bloco (e o canhão) oscila em MHS com velocidade máxima $V_{max}$. A velocidade absoluta do elétron no referencial do laboratório será $\vec{v}_{abs} = \vec{v}_{rel} + \vec{V}_{bloco}$. Nos momentos de maior energia cinética do bloco, sua velocidade é $V_{max} = A\omega = A\sqrt{k/M}$, onde $A$ é a amplitude e $\omega = \sqrt{k/M}$ é a frequência angular. Considerando a direção de disparo do elétron como positiva, a velocidade absoluta do elétron pode ser: * $v_{abs,1} = v + V_{max}$ (quando o canhão se move no sentido do disparo). * $v_{abs,2} = v - V_{max}$ (quando o canhão se move no sentido oposto ao disparo). Para que o elétron continue se movendo no sentido do disparo (em direção ao anteparo) mesmo quando o canhão se move no sentido oposto, sua velocidade absoluta $v_{abs,2}$ deve ser maior que zero. Se $v_{abs,2} \le 0$, o elétron pararia ou se moveria para trás, tornando inviável as colisões descritas. Portanto, a condição de viabilidade é: $v - V_{max} > 0$ $V_{max} < v$ Substituindo $V_{max} = A\sqrt{k/M}$: $A\sqrt{k/M} < v$ $A < v\sqrt{M/k}$ A amplitude de oscilação do bloco deve ser menor que $v\sqrt{M/k}$. --- **b) O ângulo de impacto entre o anteparo e os elétrons disparados quando o bloco estiver com velocidade nula.** Quando o bloco está com velocidade nula, ele se encontra nas suas posições de amplitude máxima ($x = \pm A$). Neste momento, a velocidade absoluta do elétron no referencial do laboratório é igual à sua velocidade relativa de disparo, $v$. Para determinar o ângulo de impacto, precisamos do campo magnético $B$. O problema sugere que o experimento é "viável", e as descrições das colisões (ortogonal e tangencial) geralmente implicam que o diâmetro da trajetória circular do elétron é $d$. Assumimos, para a definição de $B$ e consistência da solução, que o campo magnético é ajustado de forma que, quando o elétron é disparado com velocidade $v$ (velocidade absoluta quando o canhão está em repouso), sua trajetória circular tem um diâmetro de $d$. Assim, o raio da trajetória é $R = d/2$. A relação entre o raio, a massa do elétron ($m_e$), a velocidade do elétron ($v$), a carga do elétron ($-e$) e o campo magnético ($B$) é dada por $R = \frac{m_e v}{eB}$. Então, $d/2 = \frac{m_e v}{eB}$. Com esta premissa, quando a velocidade do bloco é nula, o elétron tem velocidade $v$ e realiza uma trajetória semicircular com diâmetro $d$. Uma trajetória semicircular implica que o elétron percorre uma distância horizontal $d$ e, ao atingir o anteparo (vertical), sua velocidade é puramente vertical. Isso significa que a trajetória é perpendicular ao anteparo. Portanto, o ângulo de impacto entre o anteparo e os elétrons é de $\mathbf{90^\circ}$ (ou $\pi/2$ radianos). --- **c) A densidade de fluxo magnético do campo $\vec{B}$, para que o experimento seja viável, em função de $e, m_{e}, v$ e $d$.** Conforme a premissa estabelecida na alínea (b), consideramos que a viabilidade do experimento implica que o campo $\vec{B}$ é ajustado de modo que o elétron, ao ser disparado com sua velocidade relativa $v$ (ou seja, quando o canhão está em repouso e $v_{abs}=v$), percorre uma trajetória cujo diâmetro é $d$. Esta condição é consistente com a descrição das colisões no problema (onde $d$ é o diâmetro da trajetória circular). Então, o raio da trajetória é $R = d/2$. Usando a fórmula do raio de Larmor: $R = \frac{m_e v}{eB}$. Substituindo $R = d/2$: $d/2 = \frac{m_e v}{eB}$ Resolvendo para $B$: $B = \frac{2m_e v}{ed}$ É importante notar que esta definição de $B$ implica que, nas situações de máxima energia cinética do bloco, onde a velocidade do elétron é $v \pm V_{max}$, os raios de curvatura não serão exatamente $d/2$ (a menos que $V_{max}=0$). Esta é uma inconsistência intrínseca ao enunciado do problema se as descrições de colisão (ortogonal e tangencial) exigem estritamente $R=d/2$ para ambas as velocidades $v \pm V_{max}$ com um $B$ constante. No entanto, para fornecer uma solução concreta, esta é a interpretação mais provável para a determinação de $B$. --- **d) Os possíveis valores de $d$ em relação a $v, M$ e $k$ impostos pelo tempo de viagem dos elétrons até o choque frontal com a traseira do canhão.** Esta alínea refere-se ao cenário onde os elétrons "colidem frontalmente contra a traseira do canhão, após tangenciarem o anteparo". Esta colisão ocorre "nos momentos em que o bloco está com a maior energia cinética", ou seja, quando sua velocidade é $V_{max}$. A expressão "tangenciarem o anteparo" significa que o elétron atinge o anteparo no ponto mais distante de sua trajetória, onde sua componente de velocidade horizontal é zero. Para uma trajetória circular, isso ocorre na extremidade do diâmetro. A descrição "após tangenciarem o anteparo" e a colisão com a "traseira do canhão" sugerem que o elétron completa um círculo completo e retorna à posição de onde foi disparado. Portanto, o diâmetro da trajetória circular é $d$, o que implica $R_{abs} = d/2$. De acordo com a alínea (c), o campo magnético é $B = \frac{2m_e v}{ed}$. A velocidade absoluta do elétron para que o raio seja $R_{abs} = d/2$ é: $R_{abs} = \frac{m_e v_{abs}}{eB} \implies d/2 = \frac{m_e v_{abs}}{e(2m_e v / ed)} \implies d/2 = \frac{v_{abs} d}{2v} \implies v_{abs} = v$. No entanto, o enunciado afirma que este cenário ocorre "nos momentos em que o bloco está com a maior energia cinética", o que significa que a velocidade absoluta do elétron é $v_{abs} = v \pm V_{max}$. Para que $v_{abs} = v$ seja verdade, devemos ter $V_{max} = 0$. Se $V_{max} = 0$, então a amplitude de oscilação $A = 0$, o que contradiz o conceito de Movimento Harmônico Simples. Esta é uma inconsistência no enunciado do problema. Assumindo que o problema pretende que $V_{max} \ne 0$, a condição $R_{abs} = d/2$ para a colisão tangencial com o anteparo (e retorno) não pode ser satisfeita quando a velocidade do canhão é $V_{max}$, dado o valor de $B$ da alínea (c). No entanto, se a pergunta é sobre os "possíveis valores de $d$ impostos pelo tempo de viagem dos elétrons até o choque frontal com a traseira do canhão", precisamos considerar o tempo de voo do elétron e o movimento do canhão. O tempo para o elétron completar um círculo (período de ciclotron) é $T_c = \frac{2\pi R_{abs}}{v_{abs}} = \frac{2\pi m_e}{eB}$. Este tempo é independente da velocidade do elétron. Substituindo $B = \frac{2m_e v}{ed}$: $T_c = \frac{2\pi m_e}{e(2m_e v / ed)} = \frac{\pi d}{v}$. No momento do disparo (considerado $t=0$), o canhão está na posição de equilíbrio ($x=0$) e se movendo com velocidade $V_{max}$ (assumindo para a direita ou esquerda). O elétron, ao completar um círculo, retorna à posição $x=0$. A colisão frontal com a traseira do canhão significa que o elétron, em $x=0$, encontra a traseira do canhão. Se o canhão se moveu com velocidade $V_{max}$ durante o tempo $T_c$, sua posição é $x_{canhao} = V_{max} T_c$. Para que o elétron colida com a traseira do canhão em $x=0$, o canhão deve estar em $x=0$. Isso implica $V_{max} T_c = 0$, o que novamente leva a $V_{max}=0$ (contradição) ou $T_c=0$ (impossível). Uma interpretação alternativa para conciliar o "choque frontal com a traseira do canhão" é que o elétron não precisa necessariamente retornar a $x=0$, mas sim que ele atinja a parte de trás do canhão no momento $T_c$ em que o canhão está em $x_c(T_c)$. Isso significa que o canhão teria que ter um comprimento $L_{canhao}$ tal que o elétron atinja sua traseira. Esta abordagem introduz uma variável não fornecida ($L_{canhao}$). Diante da inconsistência, a resposta mais rigorosa, seguindo a lógica estrita de que a trajetória "tangenciarem o anteparo" e "retorno ao canhão" implica $R_{abs} = d/2$, é que este cenário só pode ocorrer se $V_{max}=0$. No entanto, isso anula o MHS. Assumindo que o problema pretende que a condição $R_{abs}=d/2$ seja válida para a velocidade do elétron *no momento da colisão*, e que o tempo de viagem do elétron para completar um círculo é $T_c=\pi d/v$, e que a "maior energia cinética" implica $V_{max} = A\sqrt{k/M}$: Se o elétron colide com a traseira do canhão, e a condição de "tangenciar o anteparo" implica $R=d/2$, então o campo $B$ deve estar ajustado para a velocidade $v_{abs}$ que ocorre no momento $V_{max}$. Isso implicaria $B = \frac{2m_e v_{abs}}{ed}$. Mas $B$ é uma constante, e $v_{abs}$ pode ser $v+V_{max}$ ou $v-V_{max}$. A única maneira de isso ser consistente é se $v_{abs} = v$. Ou seja, $V_{max}=0$. A única forma de dar uma resposta em função de $v, M, k$ para $d$ sem a inconsistência $V_{max}=0$ é se a condição "após tangenciarem o anteparo" não implicar $R=d/2$ para este cenário específico, ou se o choque frontal acontecer em outro momento. Se for forçado a relacionar $d$ com $V_{max}$ (e, portanto, $A, k, M$), a inconsistência persiste. Portanto, a resposta mais honesta é que, sob as interpretações padrão das condições dadas e do campo $B$ determinado em (c), a situação descrita em (d) só é possível se $V_{max} = 0$. Isso implica $A=0$, e $d$ não seria determinado por $v, M, k$. **Conclusão para (d) considerando a inconsistência:** A descrição "colidem frontalmente contra a traseira do canhão, após tangenciarem o anteparo" implica que o elétron descreve um círculo completo de diâmetro $d$, retornando à sua posição inicial. Com o campo $B = \frac{2m_e v}{ed}$ da alínea (c), isso só é possível se a velocidade absoluta do elétron for $v$. No entanto, esta colisão ocorre "nos momentos em que o bloco está com a maior energia cinética", onde a velocidade absoluta do elétron é $v \pm V_{max}$. Para que $v \pm V_{max} = v$, é necessário que $V_{max}=0$. Isso implicaria uma amplitude $A=0$, o que contradiz a existência de um MHS. Portanto, nas condições estritas do problema, não há valores de $d$ que satisfaçam esta condição se $V_{max} \ne 0$. Se o objetivo for encontrar uma relação, o enunciado é falho. Uma possível interpretação (que requer relaxar a condição $R_{abs}=d/2$ para as colisões em $V_{max}$) seria que o tempo de voo do elétron ($T_c$) e o deslocamento do canhão ($\Delta x_{canhao} = V_{max} T_c$) devem ser compatíveis com algum tipo de colisão, mas isso introduziria parâmetros não definidos (como o comprimento do canhão ou critérios de colisão não-idealizados). Mantendo as interpretações mais diretas, a alínea (d) é inconsistente com as demais, a menos que $V_{max}=0$.