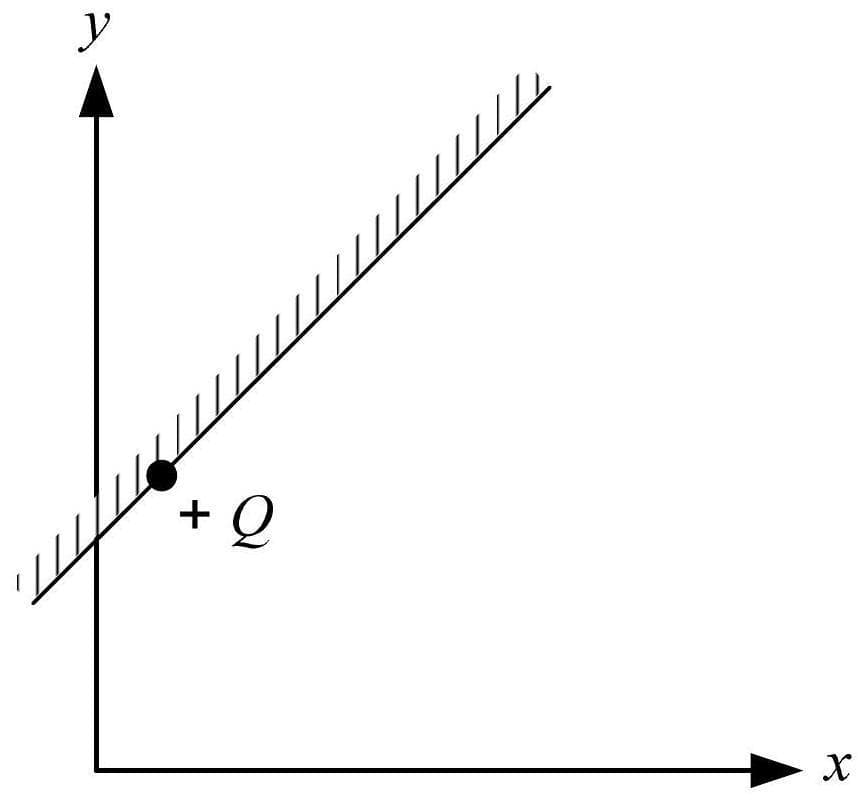
Para resolver este problema, vamos analisar cada parte separadamente, utilizando os princípios da física e da geometria vetorial. **Dados Fornecidos:** * Carga da partícula: $+Q$ * Coordenada $y$ da partícula: $y_p = 1$ (constante) * Campo magnético: $\vec{B} = (0, 0, B)$ * Equação da reta de interseção do espelho com o plano $xy$: $y = \sin(t)x + \cos^2(t)$ * Intervalo de tempo: $0 < t < \pi/2$ --- **a) As coordenadas do vetor da força magnética sofrida pela partícula.** A força magnética sofrida por uma partícula carregada em movimento é dada pela Lei de Lorentz: $\vec{F} = Q(\vec{v} \times \vec{B})$. Para calcular $\vec{F}$, precisamos determinar o vetor velocidade $\vec{v}$ da partícula. 1. **Determinar a posição da partícula:** A partícula está "presa a um espelho plano". A equação da interseção do espelho com o plano $xy$ é $y = \sin(t)x + \cos^2(t)$. Como a coordenada $y$ da partícula é sempre 1, substituímos $y=1$ na equação do espelho para encontrar a coordenada $x$ da partícula: $1 = \sin(t)x_p + \cos^2(t)$ $x_p = \frac{1 - \cos^2(t)}{\sin(t)} = \frac{\sin^2(t)}{\sin(t)}$ Considerando $0 < t < \pi/2$, temos $\sin(t) \neq 0$, então: $x_p = \sin(t)$ A coordenada $z$ da partícula não é especificada, então podemos representá-la como $z_p(t)$. Assim, o vetor posição da partícula é $\vec{r}_p(t) = (\sin(t), 1, z_p(t))$. 2. **Determinar o vetor velocidade da partícula:** O vetor velocidade é a derivada do vetor posição em relação ao tempo: $\vec{v} = \frac{d\vec{r}_p}{dt} = \left(\frac{d}{dt}(\sin(t)), \frac{d}{dt}(1), \frac{d}{dt}(z_p(t))\right)$ $\vec{v} = (\cos(t), 0, \dot{z}_p(t))$ 3. **Calcular o produto vetorial $\vec{v} \times \vec{B}$:** $\vec{v} \times \vec{B} = (\cos(t), 0, \dot{z}_p(t)) \times (0, 0, B)$ Usando a regra da mão direita ou a expansão do determinante: $\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \cos(t) & 0 & \dot{z}_p(t) \\ 0 & 0 & B \end{vmatrix} = \hat{i}(0 \cdot B - \dot{z}_p(t) \cdot 0) - \hat{j}(\cos(t) \cdot B - \dot{z}_p(t) \cdot 0) + \hat{k}(\cos(t) \cdot 0 - 0 \cdot 0)$ $= \hat{i}(0) - \hat{j}(B\cos(t)) + \hat{k}(0)$ $= (0, -B\cos(t), 0)$ 4. **Calcular o vetor da força magnética:** $\vec{F} = Q(\vec{v} \times \vec{B})$ $\vec{F} = Q(0, -B\cos(t), 0)$ $\vec{F} = (0, -QB\cos(t), 0)$ As coordenadas do vetor da força magnética sofrida pela partícula são $(0, -QB\cos(t), 0)$. --- **b) O cosseno do ângulo entre o vetor da força magnética e o plano do espelho.** Para encontrar o ângulo entre um vetor e um plano, usamos o vetor normal ao plano. O ângulo $\alpha$ entre o vetor $\vec{F}$ e o plano é o complemento do ângulo $\theta_n$ entre $\vec{F}$ e o vetor normal $\vec{n}$ ao plano. Ou seja, $\alpha = 90^\circ - \theta_n$, e, portanto, $\cos(\alpha) = \sin(\theta_n)$. 1. **Determinar o vetor normal ao plano do espelho:** A equação da interseção do espelho com o plano $xy$ é $y = \sin(t)x + \cos^2(t)$. Reorganizando, obtemos a equação do plano na forma $Ax + By + Cz + D = 0$: $\sin(t)x - y + 0z + \cos^2(t) = 0$ O vetor normal ao plano é $\vec{n} = (\sin(t), -1, 0)$. 2. **Calcular o produto escalar $\vec{F} \cdot \vec{n}$:** $\vec{F} \cdot \vec{n} = (0)(\sin(t)) + (-QB\cos(t))(-1) + (0)(0) = QB\cos(t)$ 3. **Calcular os módulos de $\vec{F}$ e $\vec{n}$:** $|\vec{F}| = \sqrt{0^2 + (-QB\cos(t))^2 + 0^2} = \sqrt{Q^2B^2\cos^2(t)}$ Como $0 < t < \pi/2$, $\cos(t) > 0$, então $|\vec{F}| = QB\cos(t)$. $|\vec{n}| = \sqrt{\sin^2(t) + (-1)^2 + 0^2} = \sqrt{\sin^2(t) + 1}$ 4. **Calcular $\cos(\theta_n)$ (cosseno do ângulo entre $\vec{F}$ e $\vec{n}$):** $\cos(\theta_n) = \frac{\vec{F} \cdot \vec{n}}{|\vec{F}| |\vec{n}|} = \frac{QB\cos(t)}{(QB\cos(t))\sqrt{\sin^2(t) + 1}} = \frac{1}{\sqrt{\sin^2(t) + 1}}$ 5. **Calcular $\cos(\alpha)$ (cosseno do ângulo entre $\vec{F}$ e o plano):** $\cos(\alpha) = \sin(\theta_n) = \sqrt{1 - \cos^2(\theta_n)}$ $\cos(\alpha) = \sqrt{1 - \left(\frac{1}{\sqrt{\sin^2(t) + 1}}\right)^2} = \sqrt{1 - \frac{1}{\sin^2(t) + 1}}$ $\cos(\alpha) = \sqrt{\frac{\sin^2(t) + 1 - 1}{\sin^2(t) + 1}} = \sqrt{\frac{\sin^2(t)}{\sin^2(t) + 1}}$ Como $0 < t < \pi/2$, $\sin(t) > 0$, então: $\cos(\alpha) = \frac{\sin(t)}{\sqrt{\sin^2(t) + 1}}$ O cosseno do ângulo entre o vetor da força magnética e o plano do espelho é $\frac{\sin(t)}{\sqrt{\sin^2(t) + 1}}$. --- **c) As coordenadas do vetor da força magnética refletido no espelho.** Para encontrar o vetor refletido $\vec{F}'$ de um vetor incidente $\vec{F}$ em um plano com vetor normal $\vec{n}$, usamos a fórmula: $\vec{F}' = \vec{F} - 2 \text{proj}_{\vec{n}} \vec{F}$ Onde $\text{proj}_{\vec{n}} \vec{F} = \frac{(\vec{F} \cdot \vec{n})}{|\vec{n}|^2} \vec{n}$. Então, $\vec{F}' = \vec{F} - 2 \frac{(\vec{F} \cdot \vec{n})}{|\vec{n}|^2} \vec{n}$. 1. **Vetores e magnitudes já calculados:** $\vec{F} = (0, -QB\cos(t), 0)$ $\vec{n} = (\sin(t), -1, 0)$ $\vec{F} \cdot \vec{n} = QB\cos(t)$ $|\vec{n}|^2 = \sin^2(t) + 1$ 2. **Substituir na fórmula do vetor refletido:** $\vec{F}' = (0, -QB\cos(t), 0) - 2 \frac{QB\cos(t)}{\sin^2(t) + 1} (\sin(t), -1, 0)$ 3. **Calcular as componentes de $\vec{F}'$:** * **Componente $x$:** $F'_x = 0 - 2 \frac{QB\cos(t)}{\sin^2(t) + 1} \sin(t) = -\frac{2QB\sin(t)\cos(t)}{\sin^2(t) + 1}$ * **Componente $y$:** $F'_y = -QB\cos(t) - 2 \frac{QB\cos(t)}{\sin^2(t) + 1} (-1)$ $F'_y = -QB\cos(t) + \frac{2QB\cos(t)}{\sin^2(t) + 1}$ Colocando $QB\cos(t)$ em evidência: $F'_y = QB\cos(t) \left( -1 + \frac{2}{\sin^2(t) + 1} \right)$ $F'_y = QB\cos(t) \left( \frac{-(\sin^2(t) + 1) + 2}{\sin^2(t) + 1} \right)$ $F'_y = QB\cos(t) \left( \frac{-\sin^2(t) - 1 + 2}{\sin^2(t) + 1} \right)$ $F'_y = QB\cos(t) \left( \frac{1 - \sin^2(t)}{\sin^2(t) + 1} \right)$ $F'_y = QB\cos(t) \frac{\cos^2(t)}{\sin^2(t) + 1} = \frac{QB\cos^3(t)}{\sin^2(t) + 1}$ * **Componente $z$:** $F'_z = 0 - 2 \frac{QB\cos(t)}{\sin^2(t) + 1} (0) = 0$ As coordenadas do vetor da força magnética refletido no espelho são: $\vec{F}' = \left( -\frac{2QB\sin(t)\cos(t)}{\sin^2(t) + 1}, \frac{QB\cos^3(t)}{\sin^2(t) + 1}, 0 \right)$