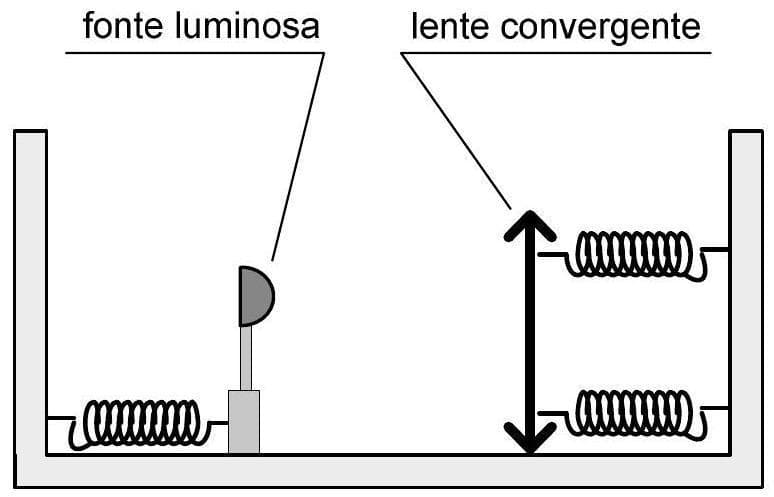
A resolução do problema envolve a análise do movimento harmônico simples dos objetos e a aplicação da equação das lentes. **1. Análise do Movimento Harmônico Simples (MHS)** Primeiramente, vamos determinar as frequências angulares e os períodos de oscilação da fonte luminosa (S) e da lente (L). * **Fonte Luminosa (S):** * Massa $m_S = 20 \mathrm{~g}$. * Presa a uma mola de constante elástica $k = 20 \mathrm{~g/s^2}$. * Frequência angular: $\omega_S = \sqrt{\frac{k}{m_S}} = \sqrt{\frac{20 \mathrm{~g/s^2}}{20 \mathrm{~g}}} = \sqrt{1 \mathrm{~s^{-2}}} = 1 \mathrm{~rad/s}$. * Período de oscilação: $T_S = \frac{2\pi}{\omega_S} = \frac{2\pi}{1} = 2\pi \mathrm{~s}$. * **Lente Convergente (L):** * Massa $m_L = 10 \mathrm{~g}$. * A figura mostra a lente presa a duas molas, o que significa que a constante elástica efetiva é $k_L = 2k = 2 \times 20 \mathrm{~g/s^2} = 40 \mathrm{~g/s^2}$. * Frequência angular: $\omega_L = \sqrt{\frac{k_L}{m_L}} = \sqrt{\frac{40 \mathrm{~g/s^2}}{10 \mathrm{~g}}} = \sqrt{4 \mathrm{~s^{-2}}} = 2 \mathrm{~rad/s}$. * Período de oscilação: $T_L = \frac{2\pi}{\omega_L} = \frac{2\pi}{2} = \pi \mathrm{~s}$. **2. Posição dos Objetos em Função do Tempo** Os objetos são colocados em contato, provocando uma elongação $A = 10 \mathrm{~cm}$ nas molas, e são soltos. Assumimos que são liberados da posição de máximo deslocamento (amplitude $A$) e se movem para longe um do outro. Vamos estabelecer um sistema de coordenadas onde a posição inicial de contato (no instante $t=0$) é $x=0$. * **Movimento da Fonte (S):** A fonte é liberada de $x=0$ e se move para a esquerda (direção negativa). Sua posição de equilíbrio é $x_{S,eq} = -A$. Como a velocidade inicial é zero, a equação de movimento é da forma $x(t) = x_{eq} + (x(0) - x_{eq})\cos(\omega t)$. $x_S(t) = -A + (0 - (-A))\cos(\omega_S t) = A(\cos(\omega_S t) - 1)$. Substituindo $\omega_S = 1 \mathrm{~rad/s}$: $x_S(t) = A(\cos(t) - 1)$. * **Movimento da Lente (L):** A lente é liberada de $x=0$ e se move para a direita (direção positiva). Sua posição de equilíbrio é $x_{L,eq} = A$. $x_L(t) = A + (0 - A)\cos(\omega_L t) = A(1 - \cos(\omega_L t))$. Substituindo $\omega_L = 2 \mathrm{~rad/s}$: $x_L(t) = A(1 - \cos(2t))$. **3. Tempo Total do Ciclo** O problema pede o tempo total do instante inicial até o instante em que a fonte e a lente se encontram novamente. Eles se encontram novamente quando $x_S(t) = x_L(t)$ para $t>0$. $A(\cos(t) - 1) = A(1 - \cos(2t))$ $\cos(t) - 1 = 1 - \cos(2t)$ $\cos(t) + \cos(2t) = 2$. Como $\cos(t) \le 1$ e $\cos(2t) \le 1$, essa igualdade só é possível se $\cos(t)=1$ e $\cos(2t)=1$. $\cos(t)=1 \implies t = 2n\pi$ para $n \in \mathbb{Z}$. Para $t=0$, eles estão em contato inicialmente. O próximo instante é para $n=1$, ou seja, $t = 2\pi \mathrm{~s}$. Portanto, o período total de análise é $[0, 2\pi]$. **4. Distância Objeto ($p$) e Condição para Imagem Virtual** A distância objeto $p(t)$ é a distância entre a fonte (objeto) e a lente. $p(t) = x_L(t) - x_S(t)$ $p(t) = A(1 - \cos(2t)) - A(\cos(t) - 1)$ $p(t) = A(1 - \cos(2t) - \cos(t) + 1)$ $p(t) = A(2 - \cos(t) - \cos(2t))$. Substituindo $\cos(2t) = 2\cos^2(t) - 1$: $p(t) = A(2 - \cos(t) - (2\cos^2(t) - 1))$ $p(t) = A(3 - \cos(t) - 2\cos^2(t))$. Com $A = 10 \mathrm{~cm}$, $p(t) = 10(3 - \cos(t) - 2\cos^2(t))$. Para uma lente convergente ($f > 0$), a imagem é virtual quando o objeto está entre o foco e a lente, ou seja, $p < f$. A distância focal é $f = 26.25 \mathrm{~cm}$. Precisamos resolver a inequação $p(t) < f$: $10(3 - \cos(t) - 2\cos^2(t)) < 26.25$ $30 - 10\cos(t) - 20\cos^2(t) < 26.25$ $20\cos^2(t) + 10\cos(t) - 3.75 > 0$. Seja $u = \cos(t)$. A inequação se torna: $20u^2 + 10u - 3.75 > 0$. Para encontrar as raízes da equação $20u^2 + 10u - 3.75 = 0$: $u = \frac{-10 \pm \sqrt{10^2 - 4(20)(-3.75)}}{2(20)}$ $u = \frac{-10 \pm \sqrt{100 + 300}}{40}$ $u = \frac{-10 \pm \sqrt{400}}{40}$ $u = \frac{-10 \pm 20}{40}$. As raízes são: $u_1 = \frac{-10 + 20}{40} = \frac{10}{40} = 0.25$. $u_2 = \frac{-10 - 20}{40} = \frac{-30}{40} = -0.75$. A parábola $20u^2 + 10u - 3.75$ tem concavidade para cima, então a inequação $20u^2 + 10u - 3.75 > 0$ é satisfeita quando $u < -0.75$ ou $u > 0.25$. Ou seja, a imagem é virtual quando $\cos(t) < -0.75$ ou $\cos(t) > 0.25$. **5. Cálculo do Tempo Total com Imagem Virtual** Analisaremos esses intervalos de $\cos(t)$ para $t \in [0, 2\pi]$. * **Condição $\cos(t) > 0.25$:** Seja $\alpha = \arccos(0.25)$. $\alpha \approx 1.3181 \mathrm{~rad}$ (aproximadamente $75.52^\circ$). No intervalo $[0, 2\pi]$, $\cos(t) > 0.25$ quando $t \in [0, \alpha)$ e $t \in (2\pi - \alpha, 2\pi]$. A duração total para esta condição é $\alpha + (2\pi - (2\pi - \alpha)) = 2\alpha$. $2\alpha \approx 2 \times 1.3181 = 2.6362 \mathrm{~s}$. * **Condição $\cos(t) < -0.75$:** Seja $\beta = \arccos(-0.75)$. $\beta \approx 2.4189 \mathrm{~rad}$ (aproximadamente $138.59^\circ$). No intervalo $[0, 2\pi]$, $\cos(t) < -0.75$ quando $t \in (\beta, 2\pi - \beta)$. A duração total para esta condição é $(2\pi - \beta) - \beta = 2\pi - 2\beta$. $2\pi - 2\beta \approx 6.2832 - 2 \times 2.4189 = 6.2832 - 4.8378 = 1.4454 \mathrm{~s}$. O tempo total em que a imagem formada é virtual é a soma dessas durações: $T_{virtual} = 2\alpha + (2\pi - 2\beta)$ $T_{virtual} \approx 2.6362 \mathrm{~s} + 1.4454 \mathrm{~s}$ $T_{virtual} \approx 4.0816 \mathrm{~s}$. Arredondando para duas casas decimais, $T_{virtual} \approx 4.08 \mathrm{~s}$. The final answer is $\boxed{4.08 \mathrm{~s}}$.