Questão sobre Ondas: Polarização
Fonte: IME-2FASE
Disciplina Física
Física
Assunto Ondas: Polarização
Ondas: Polarização
Dificuldade Médio
Médio
(IME-2FASE 2019) - Questão Médio de Física
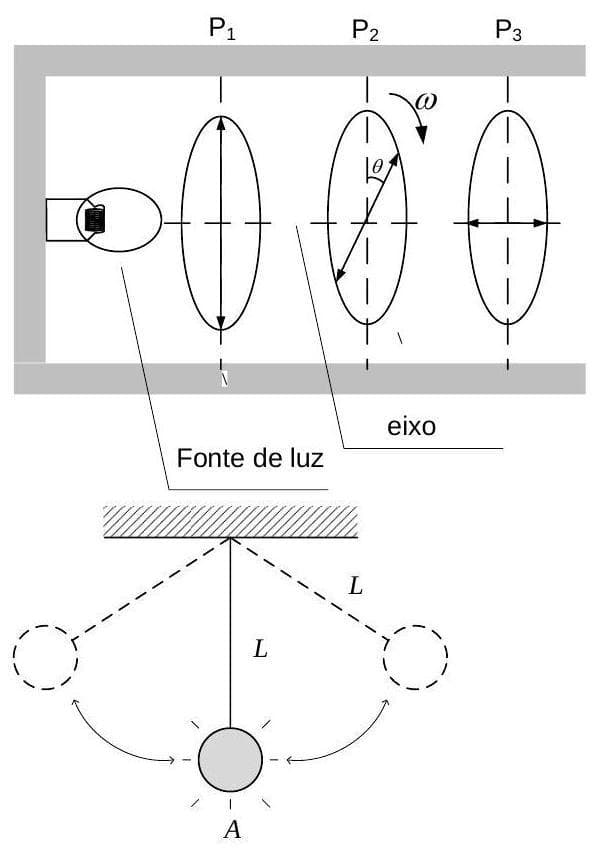
Gabarito
Aqui está uma solução discursiva e completa para o problema: --- **a) Intensidade da luz estroboscópica em função do ângulo $\theta$** Para determinar a intensidade da luz estroboscópica, precisamos aplicar a Lei de Malus em cada polarizador. Considere a intensidade da luz não polarizada da fonte como $I_{fonte}$. 1. **Após o polarizador P1:** A luz incidente em P1 é não polarizada. Após passar por P1, ela se torna polarizada linearmente na direção do plano de polarização de P1, e sua intensidade é reduzida pela metade. $I_1 = \frac{I_{fonte}}{2}$ 2. **Após o polarizador P2:** A luz incidente em P2 é polarizada na direção de P1. O ângulo entre os planos de polarização de P1 e P2 é $\theta$. Aplicando a Lei de Malus: $I_2 = I_1 \cos^2(\theta) = \left(\frac{I_{fonte}}{2}\right) \cos^2(\theta)$ 3. **Após o polarizador P3:** A luz incidente em P3 é polarizada na direção de P2. Sabemos que P1 e P3 estão com seus planos de polarização ortogonais. Isso significa que o ângulo entre os planos de P1 e P3 é de $90^\circ$. Se P1 está em um ângulo de referência $0^\circ$, P2 está em $\theta$, e P3 está em $90^\circ$. Portanto, o ângulo entre os planos de P2 e P3 é $(90^\circ - \theta)$. Aplicando novamente a Lei de Malus: $I_3 = I_2 \cos^2(90^\circ - \theta)$ Utilizando a identidade trigonométrica $\cos(90^\circ - \theta) = \sin(\theta)$: $I_3 = I_2 \sin^2(\theta)$ Substituindo a expressão para $I_2$: $I_3 = \left(\frac{I_{fonte}}{2}\right) \cos^2(\theta) \sin^2(\theta)$ 4. **Relação com $I_0$:** O problema define $I_0$ como a intensidade máxima da luz estroboscópica se os três polarizadores estivessem alinhados. Se P1, P2 e P3 estivessem alinhados (ou seja, seus planos de polarização seriam paralelos), a luz passaria por P1 e P2 (com $\theta=0^\circ$) e por P3 (com ângulo de $0^\circ$ em relação a P2) sem atenuação adicional além da inicial por P1. Nesse caso hipotético, a intensidade seria $I_{alinhado} = \frac{I_{fonte}}{2} \cos^2(0^\circ) \cos^2(0^\circ) = \frac{I_{fonte}}{2}$. Portanto, $I_0 = \frac{I_{fonte}}{2}$. Substituindo $I_0$ na expressão para $I_3$: $I(\theta) = I_0 \cos^2(\theta) \sin^2(\theta)$ Podemos simplificar esta expressão usando a identidade trigonométrica $\sin(2\theta) = 2 \sin(\theta) \cos(\theta)$: $\cos^2(\theta) \sin^2(\theta) = \frac{(2 \sin(\theta) \cos(\theta))^2}{4} = \frac{\sin^2(2\theta)}{4}$ Assim, a intensidade da luz estroboscópica em função do ângulo $\theta$ é: $\boxed{I(\theta) = I_0 \frac{\sin^2(2\theta)}{4}}$ --- **b) O comprimento $L$ do pêndulo** Para que a massa do pêndulo pareça estar parada na posição inferior (ponto A), a luz estroboscópica deve piscar (atingir sua intensidade máxima) sempre que a massa passa por esse ponto. 1. **Frequência dos flashes de luz:** A intensidade da luz é dada por $I(t) = I_0 \frac{\sin^2(2\omega t)}{4}$, pois o polarizador P2 gira com frequência angular constante $\omega$, de modo que $\theta = \omega t$. A visão humana só percebe a intensidade luminosa quando ela é máxima. A intensidade $I(t)$ é máxima quando $\sin^2(2\omega t) = 1$. Isso ocorre quando $2\omega t = \frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2}, \dots$, ou, de forma geral, $2\omega t = \frac{\pi}{2} + n\pi$, onde $n$ é um número inteiro não negativo. Os instantes de máxima intensidade são $t = \frac{\pi}{4\omega} + n\frac{\pi}{2\omega}$. O período entre dois flashes consecutivos (tempo entre máximos de intensidade) é a diferença entre dois desses instantes: $T_{flash} = \left(\frac{\pi}{4\omega} + (n+1)\frac{\pi}{2\omega}\right) - \left(\frac{\pi}{4\omega} + n\frac{\pi}{2\omega}\right) = \frac{\pi}{2\omega}$. 2. **Período de passagem do pêndulo pelo ponto A:** O pêndulo simples, de comprimento $L$, tem um período de oscilação dado por $T_{pend} = 2\pi \sqrt{\frac{L}{g}}$. A massa do pêndulo passa pelo ponto A (posição inferior) duas vezes em cada ciclo completo: uma vez indo para um lado e outra vez indo para o outro lado. Para que ela pareça "parada" no ponto A, o estroboscópio deve piscar a cada passagem pelo ponto A. Portanto, o período de flashes $T_{flash}$ deve ser igual à metade do período de oscilação do pêndulo, $T_{pend}/2$. $T_{passagem\_A} = \frac{T_{pend}}{2} = \frac{1}{2} \left(2\pi \sqrt{\frac{L}{g}}\right) = \pi \sqrt{\frac{L}{g}}$. 3. **Determinação do comprimento $L$:** Igualando o período dos flashes ao período de passagem do pêndulo pelo ponto A: $T_{flash} = T_{passagem\_A}$ $\frac{\pi}{2\omega} = \pi \sqrt{\frac{L}{g}}$ Dividindo ambos os lados por $\pi$: $\frac{1}{2\omega} = \sqrt{\frac{L}{g}}$ Elevando ambos os lados ao quadrado: $\left(\frac{1}{2\omega}\right)^2 = \frac{L}{g}$ $\frac{1}{4\omega^2} = \frac{L}{g}$ Isolando $L$: $\boxed{L = \frac{g}{4\omega^2}}$
Está montando uma prova ou lista de exercícios?
Na plataforma da Teachy é possível gerar esses materiais automaticamente, sem perder horas buscando por questões 😉
Quem viu essa questão também gostou de...
Questão
Questão
Dificuldade Médio
Fonte:
ITA
Eletricidade: Problemas de Forças e Campos Elétricos
Dificuldade Médio
Questão
Questão
Dificuldade Médio
Fonte:
UNICAMP (TODOS OS ANOS)
Impulso e Quantidade de Movimento: Colisões em uma Dimensão • 'EM13CNT306'
Dificuldade Médio
Questão
Questão
Dificuldade Médio
Fonte:
SEMSP_PROVA_SEMESTRAL_SP
Astronomia: Fases da Lua • 'EF09CI15'
Dificuldade Médio
Questão
Questão
Dificuldade Médio
Fonte:
ITA
Eletricidade: Circuitos Elétricos • 'EM13CNT308'
Dificuldade Médio
Faça parte de uma comunidade de professores direto no seu WhatsApp
Conecte-se com outros professores, receba e compartilhe materiais, dicas, treinamentos, e muito mais!
2026 - Todos os direitos reservados