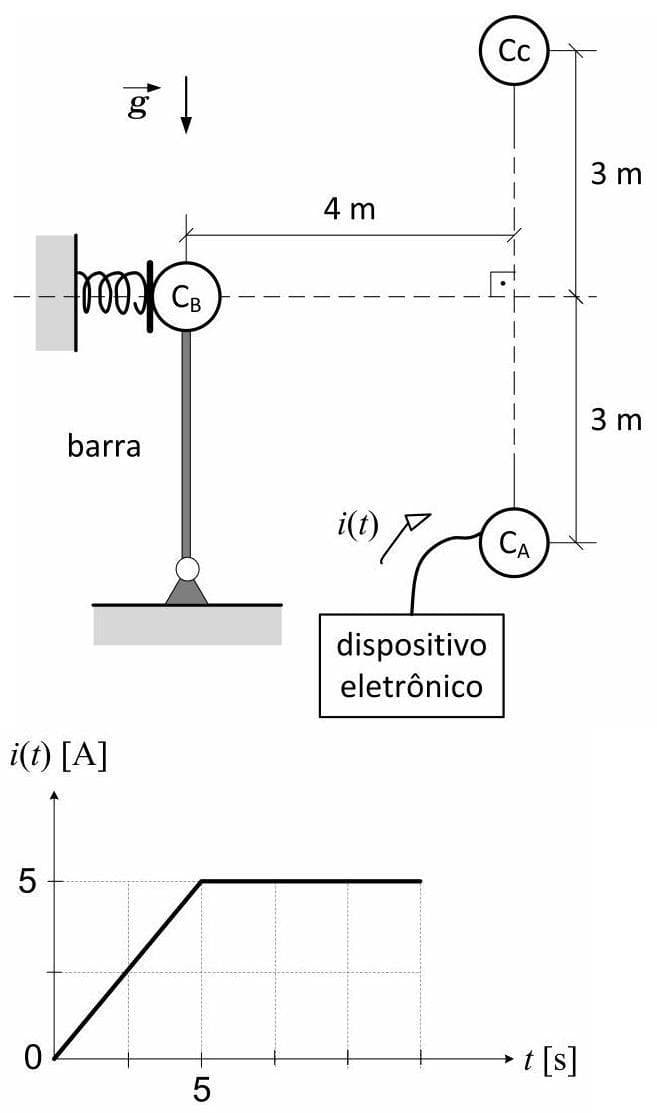
Para resolver o problema, é necessário interpretar as informações fornecidas e fazer algumas suposições razoáveis sobre a geometria do sistema e o gráfico da corrente, que não foram fornecidos. **Premissas Adotadas:** 1. **Geometria do Sistema (Figura 1):** Assumimos que os corpos $C_A$, $C_B$ e $C_C$ estão alinhados verticalmente. Para que as forças eletrostáticas contribuam para a compressão da barra vertical e para que a constante $k$ seja positiva, consideramos que $C_A$ está acima de $C_B$ e $C_C$ está abaixo de $C_B$. 2. **Distâncias:** Na ausência da Figura 1, assumimos que as distâncias entre os centros dos corpos são uniformes: $d_{AB} = d_{BC} = d$. Um valor comum para problemas desse tipo é $d = 0,5 \text{ m}$. 3. **Gráfico da Corrente (Figura 2):** Assumimos que a Figura 2 mostra uma corrente constante ao longo do tempo. Um valor típico para uma corrente de injeção em problemas didáticos, quando não especificado, é $I = 0,5 \text{ A}$. --- ### a) Determine a constante eletrostática do meio, sabendo que nas condições iniciais, a força de compressão na barra é 4 N. Para determinar a constante eletrostática $k$, analisamos as forças verticais que atuam sobre o corpo $C_B$ na situação inicial. A força de compressão na barra é a força total exercida por $C_B$ sobre a barra, que é a soma de seu peso e das componentes verticais das forças eletrostáticas. **Dados Iniciais:** * Massa do corpo $C_B$: $m = 0,2 \text{ kg}$ * Aceleração da gravidade: $g = 10 \text{ m/s}^2$ * Cargas iniciais: $Q_A = +5 \text{ C}$, $Q_B = -5 \text{ C}$, $Q_C = +30 \text{ C}$ * Força de compressão na barra: $F_{compressão} = 4 \text{ N}$ **Forças atuantes sobre $C_B$:** 1. **Peso ($P_B$):** É uma força vertical para baixo. $P_B = m \cdot g = 0,2 \text{ kg} \cdot 10 \text{ m/s}^2 = 2 \text{ N}$ (para baixo) 2. **Força Eletrostática de $C_A$ sobre $C_B$ ($F_{AB}$):** * $Q_A = +5 \text{ C}$ e $Q_B = -5 \text{ C}$. Cargas de sinais opostos se atraem. * Como $C_A$ está acima de $C_B$ (conforme premissa 1), a força $F_{AB}$ é de atração, puxando $C_B$ para cima. * A magnitude é dada pela Lei de Coulomb: $F_{AB} = k \frac{|Q_A Q_B|}{d_{AB}^2}$ * $F_{AB} = k \frac{|(+5 \text{ C})(-5 \text{ C})|}{(0,5 \text{ m})^2} = k \frac{25}{0,25} = 100k$ (para cima) 3. **Força Eletrostática de $C_C$ sobre $C_B$ ($F_{CB}$):** * $Q_C = +30 \text{ C}$ e $Q_B = -5 \text{ C}$. Cargas de sinais opostos se atraem. * Como $C_C$ está abaixo de $C_B$ (conforme premissa 1), a força $F_{CB}$ é de atração, puxando $C_B$ para baixo. * A magnitude é dada pela Lei de Coulomb: $F_{CB} = k \frac{|Q_C Q_B|}{d_{BC}^2}$ * $F_{CB} = k \frac{|(+30 \text{ C})(-5 \text{ C})|}{(0,5 \text{ m})^2} = k \frac{150}{0,25} = 600k$ (para baixo) **Cálculo da Constante Eletrostática ($k$):** A força de compressão na barra ($F_{compressão}$) é a soma vetorial das forças verticais que $C_B$ exerce sobre ela. Considerando o sentido para baixo como positivo: $F_{compressão} = P_B + F_{CB} - F_{AB}$ $4 \text{ N} = 2 \text{ N} + 600k - 100k$ $4 = 2 + 500k$ $2 = 500k$ $k = \frac{2}{500} = 0,004 \text{ N m}^2/\text{C}^2$ A constante eletrostática do meio é $\boxed{0,004 \text{ N m}^2/\text{C}^2}$. --- ### b) o novo valor da carga $Q_{\mathrm{A}}$; Nesta nova condição, a tração na barra é zero. Isso significa que a força resultante vertical sobre $C_B$ é nula. Apenas a carga $Q_A$ é alterada. **Condição:** Força de tração na barra = 0 (ou seja, força líquida vertical em $C_B$ = 0). **Cargas:** $Q_A'$ (novo valor de $Q_A$), $Q_B = -5 \text{ C}$, $Q_C = +30 \text{ C}$. As forças são as mesmas, mas $F_{AB}$ terá um novo valor ($F_{AB}'$) devido a $Q_A'$. * $P_B = 2 \text{ N}$ (para baixo) * $F_{CB} = 600k = 600 \cdot 0,004 = 2,4 \text{ N}$ (para baixo) * $F_{AB}' = k \frac{|Q_A' Q_B|}{d^2} = k \frac{|Q_A' (-5)|}{(0,5)^2} = k \frac{5|Q_A'|}{0,25} = 20k|Q_A'|$ O problema informa que cargas positivas são injetadas em $C_A$, o que significa que $Q_A'$ será positivo e maior que $Q_A$ inicial ($+5 \text{ C}$). Como $Q_B$ é negativo, a força $F_{AB}'$ continuará sendo de atração e, portanto, para cima. Equilíbrio de forças verticais (considerando para baixo como positivo): $P_B + F_{CB} - F_{AB}' = 0$ $2 \text{ N} + 2,4 \text{ N} - 20k|Q_A'| = 0$ $4,4 - 20(0,004)|Q_A'| = 0$ $4,4 - 0,08|Q_A'| = 0$ $0,08|Q_A'| = 4,4$ $|Q_A'| = \frac{4,4}{0,08} = \frac{440}{8} = 55 \text{ C}$ Como $Q_A$ aumenta devido à injeção de cargas positivas, $Q_A'$ é positivo. Portanto, o novo valor da carga $Q_A$ é $\boxed{+55 \text{ C}}$. --- ### c) o tempo necessário para o sistema chegar a este novo ponto de operação. Para determinar o tempo, precisamos saber a variação de carga em $C_A$ e a corrente injetada. **Variação da Carga em $C_A$ ($\Delta Q_A$):** $\Delta Q_A = Q_A' - Q_A = +55 \text{ C} - (+5 \text{ C}) = +50 \text{ C}$ **Corrente Injetada (extraída da Figura 2):** Conforme a premissa 3, assumimos que a Figura 2 indica uma corrente constante de $I = 0,5 \text{ A}$. A relação entre carga, corrente e tempo é: $\Delta Q = I \cdot t$ $t = \frac{\Delta Q_A}{I}$ $t = \frac{50 \text{ C}}{0,5 \text{ A}} = 100 \text{ s}$ O tempo necessário para o sistema chegar a este novo ponto de operação é $\boxed{100 \text{ s}}$.