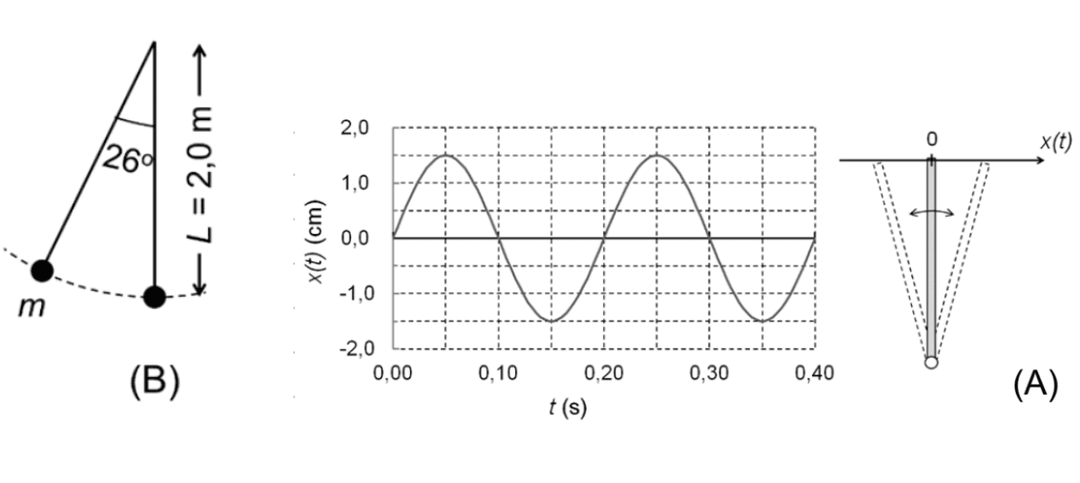
a) A velocidade escalar média $v_{em}$ é dada pela razão entre a distância percorrida pelo extremidade da haste e o tempo decorrido durante esse deslocamento; assim: $v_{em}=\frac{\text {distância percorrida}}{\text {intervalo de tempo}}=\frac{4 \times \text {amplitude}}{\text {período } \mathrm{T}}=\frac{4 \times 1,5 \mathrm{~cm}}{0,20 \mathrm{~s}}=30 \mathrm{~cm} / \mathrm{s}$ Já o módulo da velocidade média é dado pela razão da diferença entre a posição final e inicial da extremidade da haste e o tempo decorrido durante esse deslocamento; assim: $v_{m}=\frac{x(t+T)-x(\mathrm{t})}{T}=\frac{x(t)-x(\mathrm{t})}{T}=0$ b) Considerando a conservação de energia mecânica da massa na extremidade do pêndulo: $\left(E_{\text {cin }}+E_{\text {pot }}\right)_{\text {inicial }}=\left(E_{\text {cin }}+E_{\text {pot }}\right)_{\text {final }}$ temos: $0+m g h=\frac{1}{2} m v^{2}+0$ Assim, a velocidade da massa quando ela passa pelo ponto mais baixo da trajetória é: $v=\sqrt{2 g h}=\sqrt{2 g L\left(1-\cos \theta_{0}\right)}=\sqrt{2 \times\left(10 \mathrm{~m} / \mathrm{s}^{2}\right) \times(2,0 \mathrm{~m}) \times\left(1-\cos \left(26^{0}\right)\right)}$ $=\sqrt{2 \times\left(10 \mathrm{~m} / \mathrm{s}^{2}\right) \times(2,0 \mathrm{~m}) \times(1-0,90)}=2,0 \mathrm{~m} / \mathrm{s}$