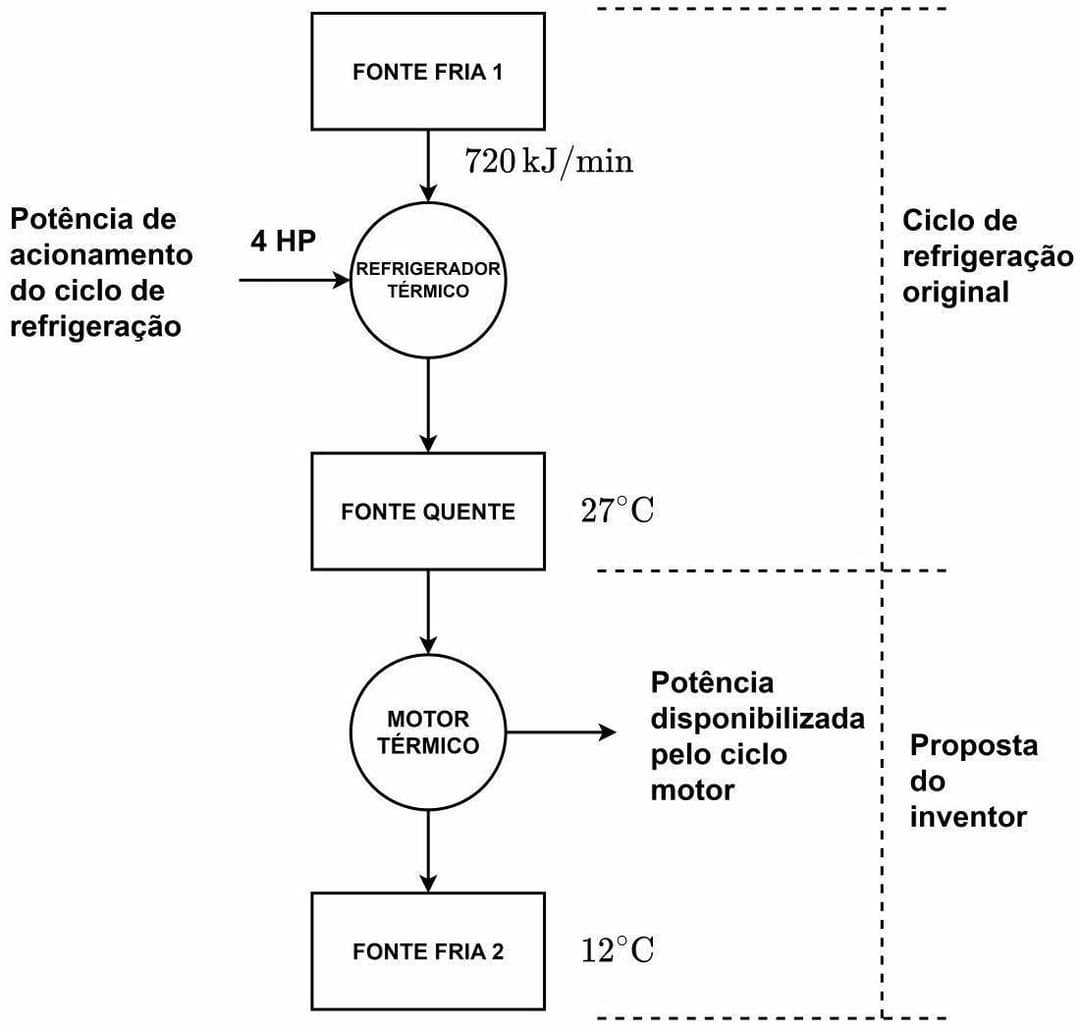
A seguir, apresenta-se a análise termodinâmica e a avaliação das proposições do inventor, bem como o cálculo da temperatura da fonte fria do ciclo de refrigeração. **Parte a) Argumento sobre a acurácia das duas proposições do inventor** Para avaliar as proposições do inventor, é necessário realizar um balanço de energia e desempenho para o sistema combinado, utilizando as leis da termodinâmica. **1. Conversão e Unificação de Unidades:** Primeiramente, convertemos todas as grandezas para unidades consistentes do Sistema Internacional (SI): * **Taxa de transferência de calor da fonte fria para o ciclo de refrigeração ($Q_{L,refrig}$):** $Q_{L,refrig} = 720 \mathrm{~kJ/min} = \frac{720 \times 1000 \mathrm{~J}}{60 \mathrm{~s}} = 12000 \mathrm{~W} = 12 \mathrm{~kW}$. * **Temperatura da fonte quente comum ($T_H$):** $T_H = 27^{\circ} \mathrm{C} = 27 + 273.15 = 300.15 \mathrm{~K}$. * **Potência de acionamento do ciclo de refrigeração ($W_{in,refrig}$):** $W_{in,refrig} = 4 \mathrm{~HP} = 4 \times (0.75 \mathrm{~kW}) = 3 \mathrm{~kW}$. * **Temperatura da fonte fria do ciclo motor ($T_{C,motor}$):** $T_{C,motor} = 12^{\circ} \mathrm{C} = 12 + 273.15 = 285.15 \mathrm{~K}$. * **Equivalência de HP:** $1 \mathrm{~HP} = 0.75 \mathrm{~kW}$. **2. Análise do Ciclo de Refrigeração:** O ciclo de refrigeração absorve calor da fonte fria e requer trabalho para rejeitar calor para a fonte quente. * Pelo balanço de energia no ciclo de refrigeração, o calor rejeitado para a fonte quente comum ($Q_{H,refrig}$) é a soma do calor absorvido da fonte fria e o trabalho de acionamento: $Q_{H,refrig} = Q_{L,refrig} + W_{in,refrig}$ $Q_{H,refrig} = 12 \mathrm{~kW} + 3 \mathrm{~kW} = 15 \mathrm{~kW}$. Este é o calor disponível para o ciclo motor. **3. Análise do Ciclo Motor Térmico:** O ciclo motor aproveita uma fração do calor rejeitado pelo ciclo de refrigeração. * **Calor de entrada no ciclo motor ($Q_{H,motor}$):** A razão de aproveitamento é $2/3$, então: $Q_{H,motor} = (2/3) \times Q_{H,refrig} = (2/3) \times 15 \mathrm{~kW} = 10 \mathrm{~kW}$. * **Desempenho máximo do ciclo motor:** O inventor menciona "condições de máximo desempenho do ciclo motor", o que implica que o motor opera como um ciclo de Carnot. A eficiência térmica de um ciclo de Carnot é dada por: $\eta_{Carnot} = 1 - \frac{T_{C,motor}}{T_H}$ $\eta_{Carnot} = 1 - \frac{285.15 \mathrm{~K}}{300.15 \mathrm{~K}} \approx 1 - 0.94998 = 0.05002 = 5.002\%$. * **Potência gerada pelo ciclo motor ($W_{out,motor}$):** A potência gerada é o produto da eficiência pelo calor de entrada: $W_{out,motor} = \eta_{Carnot} \times Q_{H,motor} = 0.05002 \times 10 \mathrm{~kW} = 0.5002 \mathrm{~kW}$. **4. Avaliação da Proposição (1) do Inventor:** * **Proposição (1): "a potência gerada é de 2 HP"** A potência máxima calculada para o motor térmico é de $0.5002 \mathrm{~kW}$. Convertendo para HP: $W_{out,motor} = 0.5002 \mathrm{~kW} \times \frac{1 \mathrm{~HP}}{0.75 \mathrm{~kW}} \approx 0.667 \mathrm{~HP}$. * **Conclusão sobre a Proposição (1):** A afirmação do inventor de que a potência gerada é de 2 HP é **inprecisa (ou falsa)**. Mesmo sob as condições ideais de máximo desempenho (ciclo de Carnot), a potência máxima que o motor térmico poderia gerar é de aproximadamente 0.67 HP, o que é significativamente menor do que os 2 HP propostos. **5. Avaliação da Proposição (2) do Inventor:** * **Calor rejeitado para o reservatório térmico adicional ($Q_{C,motor}$):** Pelo balanço de energia no ciclo motor, o calor rejeitado é o calor de entrada menos o trabalho gerado: $Q_{C,motor} = Q_{H,motor} - W_{out,motor} = 10 \mathrm{~kW} - 0.5002 \mathrm{~kW} = 9.4998 \mathrm{~kW}$. * **Potência necessária para acender as lâmpadas:** 200 lâmpadas de 50 W cada exigem uma potência total de: $P_{lâmpadas} = 200 \times 50 \mathrm{~W} = 10000 \mathrm{~W} = 10 \mathrm{~kW}$. * **Conclusão sobre a Proposição (2):** A afirmação do inventor de que a taxa de transferência de calor para o reservatório térmico adicional é capaz de prover energia equivalente para acender 200 lâmpadas de 50 W é **inprecisa (ou falsa)**. O calor rejeitado pelo motor térmico ($9.4998 \mathrm{~kW}$) é inferior à potência total requerida pelas lâmpadas ($10 \mathrm{~kW}$). Este calor seria suficiente para acender apenas $9499.8 \mathrm{~W} / 50 \mathrm{~W/lâmpada} \approx 190$ lâmpadas. --- **Parte b) Avaliação da temperatura da fonte fria do ciclo de refrigeração, em ${ }^{\circ} \mathrm{C}$.** **1. Cálculo do Coeficiente de Desempenho (COP) real do ciclo de refrigeração:** O COP real do ciclo de refrigeração é dado pela razão entre o calor absorvido da fonte fria e o trabalho de acionamento: $COP_{refrig} = \frac{Q_{L,refrig}}{W_{in,refrig}} = \frac{12 \mathrm{~kW}}{3 \mathrm{~kW}} = 4$. **2. Cálculo do COP de Carnot para o ciclo de refrigeração:** O problema informa que o $COP_{refrig}$ é $12/22$ do equivalente ao ciclo de Carnot. $COP_{refrig} = (12/22) \times COP_{Carnot,refrig}$ $4 = (12/22) \times COP_{Carnot,refrig}$ $COP_{Carnot,refrig} = 4 \times \frac{22}{12} = \frac{88}{12} = \frac{22}{3}$. **3. Determinação da temperatura da fonte fria do ciclo de refrigeração ($T_{C,refrig}$):** Para um ciclo de refrigeração de Carnot, o COP é expresso em termos das temperaturas das fontes quente e fria: $COP_{Carnot,refrig} = \frac{T_{C,refrig}}{T_H - T_{C,refrig}}$ Onde $T_H = 300.15 \mathrm{~K}$ (temperatura da fonte quente comum). Substituindo os valores conhecidos: $\frac{22}{3} = \frac{T_{C,refrig}}{300.15 \mathrm{~K} - T_{C,refrig}}$ Multiplicando em cruz: $22 \times (300.15 - T_{C,refrig}) = 3 \times T_{C,refrig}$ $6603.3 - 22 T_{C,refrig} = 3 T_{C,refrig}$ Agrupando os termos de $T_{C,refrig}$: $6603.3 = 25 T_{C,refrig}$ $T_{C,refrig} = \frac{6603.3}{25} = 264.132 \mathrm{~K}$. **4. Conversão para Celsius:** Para converter a temperatura de Kelvin para Celsius, subtraímos 273.15: $T_{C,refrig} = 264.132 - 273.15 = -9.018^{\circ} \mathrm{C}$. Arredondando para uma casa decimal, a temperatura da fonte fria do ciclo de refrigeração é: $T_{C,refrig} \approx -9.0^{\circ} \mathrm{C}$.