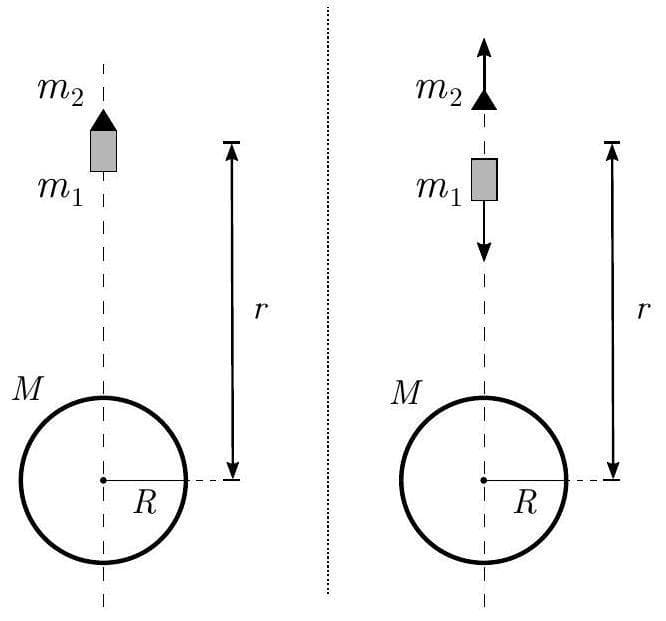
Apresentamos a solução detalhada para cada item. --- **Parte (a): O trabalho realizado pelo motor-foguete durante o $1^{o}$ estágio do seu movimento de subida.** O trabalho realizado por uma força não conservativa, como a força de propulsão do motor-foguete, é igual à variação da energia mecânica total do sistema. O sistema é composto pelo veículo espacial (motor-foguete + carga útil) e pelo planeta. 1. **Definição dos estados inicial e final:** * **Estado Inicial (lançamento):** O veículo está na superfície do planeta (distância $R$ do centro) e em repouso. * Massa total do veículo: $m_{total} = m_{1} + m_{2}$. * Energia cinética inicial: $K_{i} = 0$. * Energia potencial gravitacional inicial: $U_{i} = -\frac{G M m_{total}}{R}$. * Energia mecânica inicial: $E_{i} = K_{i} + U_{i} = -\frac{G M (m_{1} + m_{2})}{R}$. * **Estado Final (repouso na altura máxima):** O veículo atinge o repouso a uma distância $r$ do centro do planeta. * Energia cinética final: $K_{f} = 0$. * Energia potencial gravitacional final: $U_{f} = -\frac{G M m_{total}}{r}$. * Energia mecânica final: $E_{f} = K_{f} + U_{f} = -\frac{G M (m_{1} + m_{2})}{r}$. 2. **Aplicação do Teorema Trabalho-Energia:** O trabalho realizado pelo motor-foguete ($W_{motor}$) é a mudança total na energia mecânica do sistema desde o lançamento até o ponto de repouso: $W_{motor} = \Delta E_{mec} = E_{f} - E_{i}$ $W_{motor} = \left(-\frac{G M (m_{1} + m_{2})}{r}\right) - \left(-\frac{G M (m_{1} + m_{2})}{R}\right)$ $W_{motor} = G M (m_{1} + m_{2}) \left(\frac{1}{R} - \frac{1}{r}\right)$ Este trabalho é positivo, o que é consistente com a adição de energia ao sistema pelo motor para elevá-lo contra a gravidade. --- **Parte (b): A energia mecânica adquirida pelo sistema devido à explosão.** No instante da explosão, o veículo (massa $m_{1} + m_{2}$) está em repouso a uma distância $r$ do centro do planeta. A explosão é um processo interno que separa a carga útil ($m_{2}$) do motor-foguete ($m_{1}$) e imprime-lhes velocidades. A energia mecânica adquirida é a energia cinética adicional fornecida pela explosão, uma vez que a energia potencial gravitacional do sistema não muda instantaneamente no momento da explosão. 1. **Velocidade de escape da carga útil ($m_{2}$):** A carga útil $m_{2}$ é impulsionada com a velocidade mínima para escapar do campo gravitacional do planeta a partir da distância $r$. Para a velocidade de escape ($v_{esc}$), a energia mecânica final deve ser zero (apenas o suficiente para escapar para o infinito com velocidade nula). $\frac{1}{2} m_{2} v_{esc}^2 - \frac{G M m_{2}}{r} = 0$ $v_{esc}^2 = \frac{2 G M}{r}$ $v_{esc} = \sqrt{\frac{2 G M}{r}}$ 2. **Conservação do momento linear durante a explosão:** A explosão é um processo interno ao sistema $(m_{1} + m_{2})$. Como não há forças externas atuando na direção vertical durante o curto intervalo de tempo da explosão (a força gravitacional é desprezível comparada às forças da explosão), o momento linear total do sistema é conservado. * Momento linear antes da explosão: O veículo está em repouso, então $P_{antes} = (m_{1} + m_{2}) \cdot 0 = 0$. * Momento linear depois da explosão: Seja $v_{2}$ a velocidade da carga útil $m_{2}$ (igual a $v_{esc}$, para cima) e $v_{1}$ a velocidade do motor-foguete $m_{1}$ (para baixo). $P_{depois} = m_{1} v_{1} + m_{2} v_{2}$ (considerando o sentido para cima como positivo). Pela conservação do momento: $m_{1} v_{1} + m_{2} v_{esc} = 0$ $v_{1} = -\frac{m_{2}}{m_{1}} v_{esc}$ O sinal negativo indica que $m_{1}$ se move para baixo. 3. **Energia mecânica adquirida pela explosão:** A energia adquirida pelo sistema devido à explosão é a energia cinética total gerada pela explosão, pois a energia potencial gravitacional não muda instantaneamente. $\Delta E_{explosão} = K_{final} - K_{inicial}$ Como $K_{inicial} = 0$ (o veículo estava em repouso antes da explosão), $\Delta E_{explosão} = K_{final} = \frac{1}{2} m_{1} v_{1}^2 + \frac{1}{2} m_{2} v_{esc}^2$ Substituindo $v_{1}$: $\Delta E_{explosão} = \frac{1}{2} m_{1} \left(-\frac{m_{2}}{m_{1}} v_{esc}\right)^2 + \frac{1}{2} m_{2} v_{esc}^2$ $\Delta E_{explosão} = \frac{1}{2} m_{1} \frac{m_{2}^2}{m_{1}^2} v_{esc}^2 + \frac{1}{2} m_{2} v_{esc}^2$ $\Delta E_{explosão} = \frac{1}{2} \frac{m_{2}^2}{m_{1}} v_{esc}^2 + \frac{1}{2} m_{2} v_{esc}^2$ $\Delta E_{explosão} = \frac{1}{2} m_{2} v_{esc}^2 \left(\frac{m_{2}}{m_{1}} + 1\right)$ $\Delta E_{explosão} = \frac{1}{2} m_{2} v_{esc}^2 \left(\frac{m_{2} + m_{1}}{m_{1}}\right)$ Finalmente, substituindo $v_{esc}^2 = \frac{2 G M}{r}$: $\Delta E_{explosão} = \frac{1}{2} m_{2} \left(\frac{2 G M}{r}\right) \left(\frac{m_{1} + m_{2}}{m_{1}}\right)$ $\Delta E_{explosão} = \frac{G M m_{2} (m_{1} + m_{2})}{r m_{1}}$