Questão sobre Gases: Equação Geral
Fonte: IME-2FASE
Disciplina Química
Química
Assunto Gases: Equação Geral
Gases: Equação Geral
Dificuldade Médio
Médio
(IME-2FASE 2019) - Questão Médio de Química
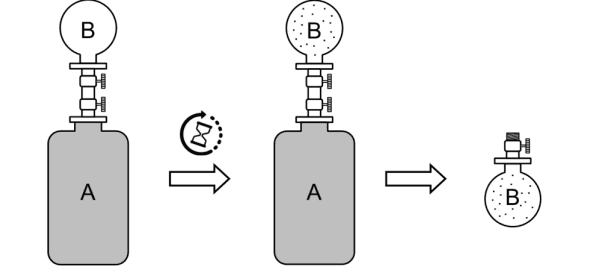
Gabarito
Para calcular o número de mols de $\mathrm{CO}_{2}$ que migraram para o recipiente B em função de $n$, devemos considerar o equilíbrio entre a fase gasosa (no recipiente B) e a fase aquosa (no recipiente A). **Dados Fornecidos:** * Temperatura ($T$) = 300 K * Constante de Henry ($K_H$) = $1/30 \text{ atm}^{-1}$ (para $x_{\mathrm{CO}_2} = K_H \cdot P_{\mathrm{CO}_2}$) * Volume do recipiente B ($V_B$) = 1,64 L * Massa de água = 1800 g * Constante dos gases ideais ($R$) = $0,082 \text{ L atm mol}^{-1} \text{ K}^{-1}$ * Número total de mols de $\mathrm{CO}_2$ = $n$ **1. Mols de Água:** Primeiramente, calculamos o número de mols de água presente, usando sua massa molar ($M_{H_2O} = 18 \text{ g/mol}$): $n_{H_2O} = \frac{\text{Massa de água}}{M_{H_2O}} = \frac{1800 \text{ g}}{18 \text{ g/mol}} = 100 \text{ mol}$ **2. Relação entre Pressão Parcial de $\mathrm{CO}_2$ e Fração Molar (Lei de Henry):** A Lei de Henry relaciona a pressão parcial do gás ($P_{\mathrm{CO}_2}$) com sua fração molar na solução ($x_{\mathrm{CO}_2}$). A constante $K_H$ é dada na forma $x_{\mathrm{CO}_2} = K_H \cdot P_{\mathrm{CO}_2}$. Portanto, podemos expressar a pressão parcial como: $P_{\mathrm{CO}_2} = \frac{x_{\mathrm{CO}_2}}{K_H} = \frac{x_{\mathrm{CO}_2}}{1/30 \text{ atm}^{-1}} = 30 \cdot x_{\mathrm{CO}_2}$ A fração molar de $\mathrm{CO}_2$ na fase aquosa é definida como: $x_{\mathrm{CO}_2} = \frac{n_{\mathrm{CO}_2, aq}}{n_{\mathrm{CO}_2, aq} + n_{H_2O}}$ Onde $n_{\mathrm{CO}_2, aq}$ é o número de mols de $\mathrm{CO}_2$ dissolvido na água. Substituindo $n_{H_2O}$: $P_{\mathrm{CO}_2} = 30 \cdot \frac{n_{\mathrm{CO}_2, aq}}{n_{\mathrm{CO}_2, aq} + 100}$ (Equação 1) **3. Relação entre Pressão Parcial de $\mathrm{CO}_2$ e Mols na Fase Gasosa (Lei dos Gases Ideais):** No recipiente B, o $\mathrm{CO}_2$ se comporta como um gás ideal. Usamos a Lei dos Gases Ideais ($PV=nRT$): $P_{\mathrm{CO}_2} \cdot V_B = n_{\mathrm{CO}_2, gas} \cdot R \cdot T$ Onde $n_{\mathrm{CO}_2, gas}$ é o número de mols de $\mathrm{CO}_2$ na fase gasosa no recipiente B. Isolando $P_{\mathrm{CO}_2}$: $P_{\mathrm{CO}_2} = \frac{n_{\mathrm{CO}_2, gas} \cdot R \cdot T}{V_B}$ Substituindo os valores conhecidos: $P_{\mathrm{CO}_2} = \frac{n_{\mathrm{CO}_2, gas} \cdot (0,082 \text{ L atm mol}^{-1} \text{ K}^{-1}) \cdot (300 \text{ K})}{1,64 \text{ L}}$ $P_{\mathrm{CO}_2} = \frac{n_{\mathrm{CO}_2, gas} \cdot 24,6}{1,64} = 15 \cdot n_{\mathrm{CO}_2, gas}$ (Equação 2) **4. Condição de Equilíbrio:** No equilíbrio, a pressão parcial de $\mathrm{CO}_2$ na fase gasosa (recipiente B) é igual à pressão parcial de $\mathrm{CO}_2$ em equilíbrio com a solução aquosa (recipiente A). Portanto, igualamos a Equação 1 e a Equação 2: $30 \cdot \frac{n_{\mathrm{CO}_2, aq}}{n_{\mathrm{CO}_2, aq} + 100} = 15 \cdot n_{\mathrm{CO}_2, gas}$ Dividindo ambos os lados por 15: $2 \cdot \frac{n_{\mathrm{CO}_2, aq}}{n_{\mathrm{CO}_2, aq} + 100} = n_{\mathrm{CO}_2, gas}$ (Equação 3) **5. Balanço de Massa para o $\mathrm{CO}_2$:** O número total de mols de $\mathrm{CO}_2$ é $n$. No equilíbrio, esses mols estão distribuídos entre a fase aquosa e a fase gasosa: $n = n_{\mathrm{CO}_2, aq} + n_{\mathrm{CO}_2, gas}$ Podemos expressar $n_{\mathrm{CO}_2, aq}$ em termos de $n$ e $n_{\mathrm{CO}_2, gas}$: $n_{\mathrm{CO}_2, aq} = n - n_{\mathrm{CO}_2, gas}$ (Equação 4) **6. Substituição e Resolução:** Substituímos a Equação 4 na Equação 3: $2 \cdot \frac{n - n_{\mathrm{CO}_2, gas}}{(n - n_{\mathrm{CO}_2, gas}) + 100} = n_{\mathrm{CO}_2, gas}$ Para simplificar a notação, seja $N_B = n_{\mathrm{CO}_2, gas}$ (o número de mols de $\mathrm{CO}_2$ que migraram para o recipiente B): $2(n - N_B) = N_B(n - N_B + 100)$ $2n - 2N_B = nN_B - N_B^2 + 100N_B$ Rearranjando os termos para formar uma equação quadrática na forma $aN_B^2 + bN_B + c = 0$: $N_B^2 - 2N_B - nN_B - 100N_B + 2n = 0$ $N_B^2 - (2 + n + 100)N_B + 2n = 0$ $N_B^2 - (n + 102)N_B + 2n = 0$ Usamos a fórmula quadrática $N_B = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$, onde $a=1$, $b=-(n+102)$, e $c=2n$: $N_B = \frac{(n+102) \pm \sqrt{(-(n+102))^2 - 4(1)(2n)}}{2(1)}$ $N_B = \frac{(n+102) \pm \sqrt{(n+102)^2 - 8n}}{2}$ $N_B = \frac{(n+102) \pm \sqrt{n^2 + 2 \cdot n \cdot 102 + 102^2 - 8n}}{2}$ $N_B = \frac{(n+102) \pm \sqrt{n^2 + 204n + 10404 - 8n}}{2}$ $N_B = \frac{(n+102) \pm \sqrt{n^2 + 196n + 10404}}{2}$ **7. Análise das Raízes:** Devemos escolher a raiz que tem significado físico. O número de mols de $\mathrm{CO}_2$ na fase gasosa ($N_B$) deve ser menor que o número total de mols de $\mathrm{CO}_2$ ($n$). A raiz com o sinal '+' no numerador resultaria em $N_B > n$ (um valor fisicamente impossível, pois a quantidade de gás não pode ser maior que a quantidade total de gás inicial). Portanto, a raiz correta é com o sinal '-': $n_{\mathrm{CO}_2, gas} = \frac{(n+102) - \sqrt{n^2 + 196n + 10404}}{2}$ Este é o número de mols de $\mathrm{CO}_2$ que migraram para o recipiente B em função de $n$. The final answer is $\boxed{n_{CO_2, gas} = \frac{(n+102) - \sqrt{n^2 + 196n + 10404}}{2}}$.
Está montando uma prova ou lista de exercícios?
Na plataforma da Teachy é possível gerar esses materiais automaticamente, sem perder horas buscando por questões 😉
Quem viu essa questão também gostou de...
Questão
Questão
Dificuldade Fácil
Fonte:
Teachy
Reações: Balanceamento • 'EM13CNT101'
Dificuldade Fácil
Questão
Questão
Dificuldade Médio
Fonte:
UNICISAL
Termoquímica: entalpia • 'EM13CNT101'
Dificuldade Médio
Questão
Questão
Dificuldade Fácil
Fonte:
UFTM
Reações: Balanceamento de Equação Redox • 'EM13CNT101'
Dificuldade Fácil
Questão
Questão
Dificuldade Médio
Fonte:
UENP
Equilíbrio: Le Chatelier
Dificuldade Médio
Faça parte de uma comunidade de professores direto no seu WhatsApp
Conecte-se com outros professores, receba e compartilhe materiais, dicas, treinamentos, e muito mais!
2026 - Todos os direitos reservados