Questão sobre Equilíbrio: Pressões Parciais
Fonte: IME-2FASE
Disciplina Química
Química
BNCC 'EM13CNT301'
'EM13CNT301'
Assunto Equilíbrio: Pressões Parciais
Equilíbrio: Pressões Parciais
Dificuldade Médio
Médio
(IME-2FASE 2016) - Questão Médio de Química
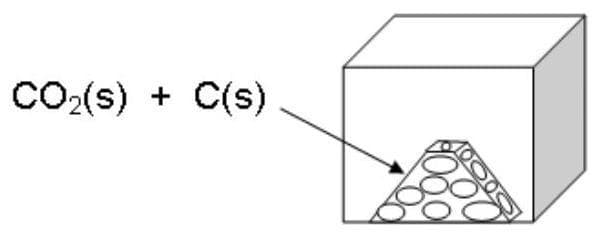
Gabarito
**Cálculo da Constante de Equilíbrio, Kp, a 1000 K:** 1. **Dados iniciais:** * Volume do reservatório (V) = 6,0 L * Massa inicial de CO₂ = 79,2 g * Massa específica da fase gasosa a 1000 K ($\rho_{\text{gás}}$) = 14 g/L * Temperatura (T) = 1000 K * Constante dos gases ideais (R) = 0,08206 L atm mol⁻¹ K⁻¹ 2. **Massa molar dos gases:** * M(CO₂) = 12,01 + 2 * 16,00 = 44,01 g/mol * M(CO) = 12,01 + 16,00 = 28,01 g/mol 3. **Cálculo da massa total de gás no equilíbrio a 1000 K:** $m_{\text{total, gás}} = \rho_{\text{gás}} \times V = 14 \text{ g/L} \times 6,0 \text{ L} = 84 \text{ g}$ 4. **Cálculo dos mols iniciais de CO₂:** $n_{\text{CO}_{2}, \text{inicial}} = \frac{79,2 \text{ g}}{44,01 \text{ g/mol}} = 1,800 \text{ mol}$ 5. **Montagem da tabela ICE (Início, Mudança, Equilíbrio) em termos de mols:** Seja 'x' o número de mols de CO₂ que reagem. $$\mathrm{CO}_{2}(\mathrm{~g})+\mathrm{C}(\mathrm{s}) \rightleftarrows 2 \mathrm{CO}(\mathrm{g})$$ | Espécie | Início (mol) | Mudança (mol) | Equilíbrio (mol) | | :------------- | :----------- | :------------ | :--------------- | | CO₂(g) | 1,800 | -x | 1,800 - x | | C(s) | (excesso) | -x | (excesso - x) | | CO(g) | 0 | +2x | 2x | 6. **Cálculo de 'x' a partir da massa total de gás no equilíbrio:** A massa total de gás no equilíbrio é a soma das massas de CO₂ e CO: $m_{\text{total, gás}} = n_{\text{CO}_{2}, \text{eq}} \times M_{\text{CO}_{2}} + n_{\text{CO}, \text{eq}} \times M_{\text{CO}}$ $84 \text{ g} = (1,800 - x) \times 44,01 \text{ g/mol} + (2x) \times 28,01 \text{ g/mol}$ $84 = 79,218 - 44,01x + 56,02x$ $84 = 79,218 + 12,01x$ $12,01x = 84 - 79,218$ $12,01x = 4,782$ $x = \frac{4,782}{12,01} \approx 0,39817 \text{ mol}$ 7. **Cálculo dos mols das espécies gasosas no equilíbrio:** $n_{\text{CO}_{2}, \text{eq}} = 1,800 - 0,39817 = 1,40183 \text{ mol}$ $n_{\text{CO}, \text{eq}} = 2 \times 0,39817 = 0,79634 \text{ mol}$ 8. **Cálculo das pressões parciais no equilíbrio (P = nRT/V):** $P_{\text{CO}_{2}} = \frac{n_{\text{CO}_{2}, \text{eq}} \times R \times T}{V} = \frac{1,40183 \text{ mol} \times 0,08206 \text{ L atm mol}^{-1} \text{ K}^{-1} \times 1000 \text{ K}}{6,0 \text{ L}}$ $P_{\text{CO}_{2}} = \frac{114,99}{6,0} \approx 19,165 \text{ atm}$ $P_{\text{CO}} = \frac{n_{\text{CO}, \text{eq}} \times R \times T}{V} = \frac{0,79634 \text{ mol} \times 0,08206 \text{ L atm mol}^{-1} \text{ K}^{-1} \times 1000 \text{ K}}{6,0 \text{ L}}$ $P_{\text{CO}} = \frac{65,34}{6,0} \approx 10,890 \text{ atm}$ 9. **Cálculo de Kp a 1000 K:** A expressão da constante de equilíbrio em termos de pressões parciais para a reação é: $K_p = \frac{(P_{\text{CO}})^2}{P_{\text{CO}_{2}}}$ (o carvão, C(s), sendo sólido, não entra na expressão de Kp) $K_p = \frac{(10,890)^2}{19,165} = \frac{118,5921}{19,165} \approx 6,188$ Arredondando para três algarismos significativos, $K_p \approx 6,19$. **Determinação se a reação é exotérmica ou endotérmica:** * **Comparação dos valores de Kp em diferentes temperaturas:** * A 1000 K, calculamos $K_p = 6,19$. * A 1100 K, foi fornecido que $K_p = 22$. * **Análise da tendência:** Observa-se que, ao aumentar a temperatura de 1000 K para 1100 K, o valor da constante de equilíbrio ($K_p$) aumenta de 6,19 para 22. * **Justificativa com base no Princípio de Le Chatelier:** De acordo com o Princípio de Le Chatelier, para uma reação endotérmica (ΔH > 0), um aumento na temperatura favorece o sentido direto da reação (formação de produtos) para absorver o calor adicionado. Isso resulta em um aumento na concentração/pressão dos produtos e uma diminuição na concentração/pressão dos reagentes, o que leva a um aumento no valor da constante de equilíbrio ($K_p$). Inversamente, para uma reação exotérmica (ΔH < 0), um aumento na temperatura favoreceria o sentido inverso, diminuindo o valor de $K_p$. * **Conclusão:** Como o valor de $K_p$ aumenta com o aumento da temperatura, a reação entre o $\mathrm{CO}_{2}(\mathrm{~g})$ e o $\mathrm{C}(\mathrm{s})$ é **endotérmica**.
Está montando uma prova ou lista de exercícios?
Na plataforma da Teachy é possível gerar esses materiais automaticamente, sem perder horas buscando por questões 😉
Quem viu essa questão também gostou de...
Questão
Questão
Dificuldade Fácil
Fonte:
Teachy
Reações: Balanceamento • 'EM13CNT101'
Dificuldade Fácil
Questão
Questão
Dificuldade Médio
Fonte:
UNICISAL
Termoquímica: entalpia • 'EM13CNT101'
Dificuldade Médio
Questão
Questão
Dificuldade Fácil
Fonte:
UFTM
Reações: Balanceamento de Equação Redox • 'EM13CNT101'
Dificuldade Fácil
Questão
Questão
Dificuldade Médio
Fonte:
UENP
Equilíbrio: Le Chatelier
Dificuldade Médio
Faça parte de uma comunidade de professores direto no seu WhatsApp
Conecte-se com outros professores, receba e compartilhe materiais, dicas, treinamentos, e muito mais!
2025 - Todos os direitos reservados